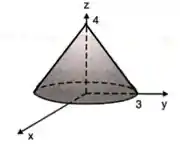
Questão 2) Determine a função que representa o cone circular reto da figura:
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nessa questão temos que determinar uma função que descreve um cone como descrito na figura.
A ideia é curta, mas será que é simples? 🤔
Primeiro de tudo temos que analisar a o gráfico da figura, assim podemos concluir três coisas: a primeira é que o cone é voltado com a boca para baixo, ou seja, quanto menor o valor de , maior é o seu raio.
A segunda coisa é que quando é formado uma circunferência de raio .
E por último, quando e são iguais a , é igual a , atingindo o maior valor para o gráfico.
A gente precisa tomar essas conclusões pra poder formular a nossa função!
Bora lá? 😁
Passo 2
A função que descreve um cone qualquer com o bico voltado para cima, é
Lembra das três observações que fizemos no passo 1. Vamos verificar se essa equação bate com elas.
A primeira dela já foi satisfeita quando acrescentamos o sinal negativo na raiz, isso mostra que a concavidade do gráfico é voltada para baixo.
vamos analisar a terceira condição: “quando e são iguais a , é igual a ”
Se fizermos e iguais a , temos
Não satisfez nossa condição, então temos que acrescentar um valor no lado direito da função para forçar a dar quando e são .
Simplesmente se somarmos , vamos obter
Vamos verificar novamente? Fazendo
Pronto! Temos duas de três condições satisfeitas!
Tranquilo até aqui? 👀
Passo 3
Agora, para a última condição, vimos que quando , deve obter uma circunferência de raio , ou seja, devemos obter a equação .
Vamos verificar se nossa função satisfaz essa condição
Elevando os dois lados ao quadrado pra eliminar a raiz, temos
Quase conseguimos! Não podemos mexer no da função, pois ele garante a condição que vimos anteriormente.
Então o que podemos fazer é acrescentar um fator multiplicativo na raiz, veja só
Fazendo , temos
Passando o para o outro lado dividindo e elevando os dois lados ao quadrado para eliminar a raiz, temos
Assim, vemos que tem que ser igual a , ou seja
Tirando a raiz dos dois lados, temos
Assim a gente define a função que descreve o gráfico da figura como
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
