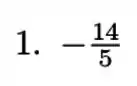
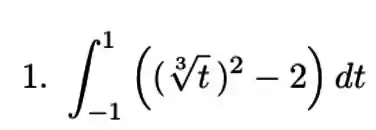
Passo 1
Vamos lá! Pra começar a resolver isso vamos separar essa integral em duas.
Vamos lembrar que , então
Passo 2
Agora precisamos encontrar as primitivas de e 1 . Para a primeira integral temos:
E para a segunda
Passo 3
Voltando para o problema original basta a gente aplicar os resultados que encontramos
Resposta
Exercícios de Livros Relacionados
Calcule a integral. ∫ 0 2 x 2 + x 5d x
19 - 44 Calcule a integral 30 .∫ 0 2 y - 1 2 y + 1d y
Calcule a integralint_(pi)^(2 pi) cos theta d theta
Calcule a integral ∫ 1 2 4 + u 2 u 3d u
Calcule a integral ∫ - 1 1 e u + 1d u