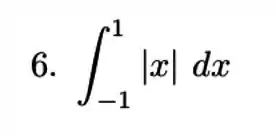
Passo 1
Aqui temos que ficar atentos ao módulo já que:
Então como resolvemos isso?
Temos que fazer
e depois
E em seguida somar as duas
Então vamos lá
E
Passo 2
Agora basta somarmos os resultados das integrais
Resposta
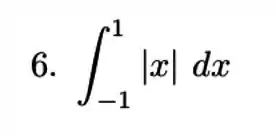
Aqui temos que ficar atentos ao módulo já que:
Então como resolvemos isso?
Temos que fazer
e depois
E em seguida somar as duas
Então vamos lá
E
Agora basta somarmos os resultados das integrais