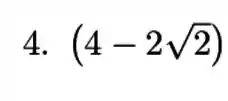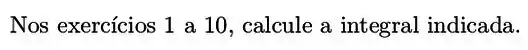
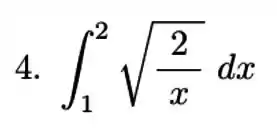
Passo 1
Vamos primeiro tirar a constante da integral
Lembrando que
Passo 2
Agora vamos encontrar a primitiva e substituir os limites
Passo 3
Só falta substituir os valores na expressão inicial
Resposta
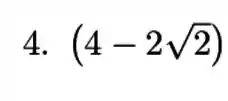
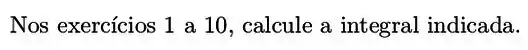
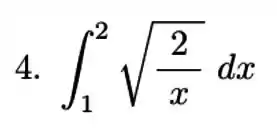
Vamos primeiro tirar a constante da integral
Lembrando que
Agora vamos encontrar a primitiva e substituir os limites
Só falta substituir os valores na expressão inicial