Integrais Indefinidas
Calcule a integral
E esboce a região cuja área a integral representa.
Passo 1
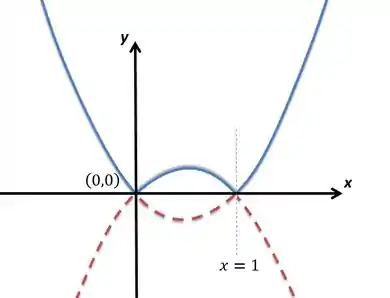
Vamos começar pensando no desenho desse módulo de parábola. O termo tem duas raízes nos seguintes pontos:
Como o termo que multiplica o é negativo, vemos que essa parábola tem boca para baixo. Nessas condições, vemos que só é positivo entre suas raízes e negativo no resto. Como tratamos do módulo dessa parábola, o gráfico será o oposto da parábola quando ela é negativa e o próprio gráfico quando é positiva:
Será algo assim o seu gráfico:
Passo 2
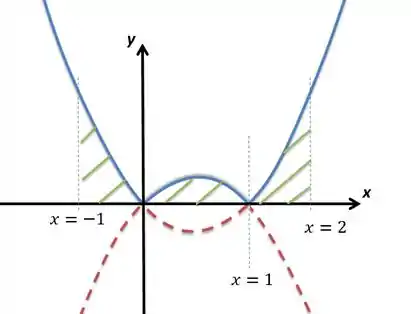
Pela integral pedida, devemos analisar em qual região do domínio encontram-se os limites de integração. A integral pedida vai de , o que significa que passa por duas regiões onde o gráfico é invertido e uma onde é ele mesmo :
A integral acaba sendo essa área aqui:
