Teorema Fundamental do Cálculo
Considere:
Onde é a função cujo gráfico é dado abaixo:
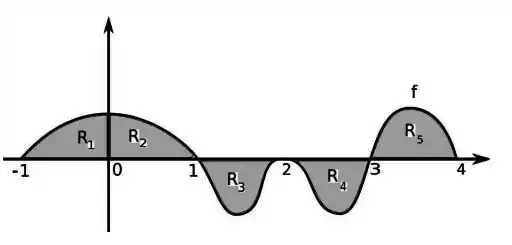
Sabendo que as áreas das regiões , , , e são:
.
Calcule , , , , e .
Passo 1
Aplicando o teorema fundamental do cálculo, temos:
Ou seja, a função nos dá a área do gráfico de entre os pontos e .
Para os pontos que ele quer, temos:
Como é área entre e sabemos que é zero, portanto:
Passo 2
Pela definição da função e dos dados, temos:
Logo, temos que:
Passo 3
Aplicando a mesma lógica para o ponto seguinte, temos:
Para o ponto seguinte temos:
Consequentemente, para temos:
Pela troca de sinal das regiões, temos:
Seguindo com a solução:
Pela mesma lógica anterior:
Continuando:
Resposta
Exercícios de Livros Relacionados
Calcule a integral. ∫ 0 2 x 2 + x 5d x
19 - 44 Calcule a integral 30 .∫ 0 2 y - 1 2 y + 1d y
Calcule a integralint_(pi)^(2 pi) cos theta d theta
Calcule a integral ∫ 1 2 4 + u 2 u 3d u
Calcule a integral ∫ - 1 1 e u + 1d u