UFSC – Cálculo 1 – Lista 4.3 – Questão 2a
Calcule as integrais definidas abaixo. Sugestão: veja que todas as integrais indefinidas necessárias já foram calculadas no exercício 7 da lista de exercícios 4.2
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Essa questão é da lista 4.3 e pergunta para calcular essa integral aqui:
e foi dado uma sugestão: que usássemos o resultado da integral indefinida no exercício 7 da lista 4.2
Bom, mas o que uma coisa tem a ver com a outra? É que a integral indefinida não tem limites de integração. Já a integral definida tem limites, e após integrar a função (com as técnicas que já vimos na lista 4.2) precisamos substituir os limites no resultado que encontramos
Por exemplo, digamos que é a primitiva da função , e queremos saber a integral de no intervalo fechado :
Tudo bem até aqui?
Então a ideia é resgatar o resultado da integral indefinida lá do exercício 7 da lista 4.2 e aplicar os limites de integração dados! Lembrando que o resultado é a primitiva aplicada no limite superior menos no limite inferior!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Resgatando o resultado da questão 7ª da lista 4.2:
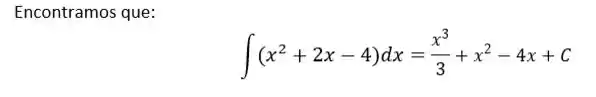A integral definida que queremos calcular é
Então vamos usar o resultado obtido (retirando aquele do final, porque estamos calculando uma definida) e aplicar nos limites de integração:
Tranquilo?
Passo 3
Agora vamos aplicar os limites:
Beleza? E é isso! O resultado dessa integral definida é !
Espero ter ajudado! Vamos para a próxima?