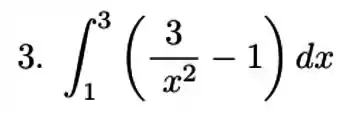
Passo 1
Então vamos começar. Para resolver isso vamos separar essa integral em duas e tirar as constantes da jogada.
Ufa! Essa foi simples.
Passo 2
Agora, vamos resolver as integrais separadamente e aplicar os limites de integração
Passo 3
Por último, vamos aplicar os valores na expressão inicial
Resposta
Exercícios de Livros Relacionados
Calcule a integral. ∫ 0 2 x 2 + x 5d x
19 - 44 Calcule a integral 30 .∫ 0 2 y - 1 2 y + 1d y
Calcule a integralint_(pi)^(2 pi) cos theta d theta
Calcule a integral ∫ 1 2 4 + u 2 u 3d u
Calcule a integral ∫ - 1 1 e u + 1d u