Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema Fundamental do Cálculo – Integral Definida

Ver Teoria
Exercício 1112345678910121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980

Enunciado

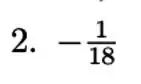
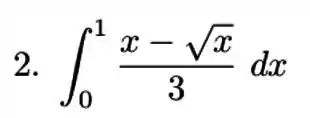
Passo 1

Para começar vamos tirar a constante de dentro da integral e separa-la em duas.

∫ 0 1 x - x 3 d x = 1 3 ∫ 0 1 x - x d x

= 1 3 ∫ 0 1 ( x - x ) d x = 1 3 ∫ 0 1 x d x - ∫ 0 1 x   d x  

Passo 2

Agora, vamos resolver separadamente as duas integrais. Vamos começar encontrando a primitiva da primeira

∫ 0 1 x = x 2 2 0 1

E agora vamos encontrar a primitiva da segunda integral, lembrando que x = x 1 / 2

∫ 0 1 x = ∫ 0 1 x 1 2 = x 1 2 + 1 1 + 1 2   0 1

∫ 0 1 x = x 3 2 3 2   0 1 = 2 3 x 3 2   0 1

Passo 3

Já encontramos as primitivas, agora temos que aplicar os limites de integração

x 2 2 0 1 = 1 2 2 - 0 2 2 = 1 2

E

2 3 x 3 2   0 1 = 2 3 1 3 2 - 2 3 0 3 2 = 2 3

Passo 4

Por último, vamos substituir os valores no problema inicial:

∫ 0 1 x - x 3 d x = 1 3 ∫ 0 1 x d x - ∫ 0 1 x   d x  

∫ 0 1 x - x 3 d x = 1 3 1 2 - 2 3

∫ 0 1 x - x 3 d x = - 1 18

Resposta

Exercícios de Livros Relacionados

Calcule a integral. ∫ 0 2 x 2 + x 5d x
19 - 44 Calcule a integral 30 .∫ 0 2 y - 1 2 y + 1d y
Calcule a integralint_(pi)^(2 pi) cos theta d theta
Calcule a integral ∫ 1 2 4 + u 2 u 3d u
Calcule a integral ∫ - 1 1 e u + 1d u