UFSCAR – Cálculo 1 – P3 – Questão 2a
Calcule as seguintes integrais
Passo 1
Oi pessoal, tudo bem? O problema nos deu essa integral aqui para resolver
Você percebe que ali dentro tem um módulo? Então: sempre que você encontrar a função módulo precisa parar, respirar e separar essa coisa em duas partes!
Isso mesmo! A função modular é uma função definida por partes, assim
E isso também serve para todas as ‘famílias’ de funções modulares! Inclusive a nossa que é uma parábola!
Mas você deve estar se perguntando: a integração é entre , por que preciso fazer isso? Eu te respondo! Note que dentro do nosso módulo tem um , isso significa que a função foi deslocada para direita em unidades!
Sendo assim, o local onde antes a função era partida (no caso ) agora é entre , e nosso intervalo de integração passa pelo , então precisamos tomar cuidado!
Então a ideia aqui é o seguinte: esboçar essa função modular em um gráfico para poder identificar onde há essa troca de cara de função, e como isso afeta nossa integral e depois partir para a integração!
Mas relaxa, vou fazer com você!
Passo 2
Vamos começar esboçando o integrando sem o módulo
É uma parábola bem comum: boca para cima, corta o eixo em , e tem raízes iguais a e :
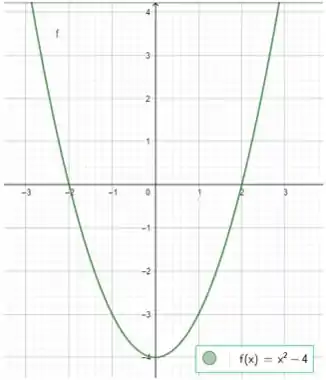
O que será que acontece com o gráfico quando colocamos o módulo na função? O módulo tem o poder de trazer toda parte da função que está embaixo para cima!
Então toda aquela parte entre as raízes vai passar para cima do eixo ! Saca só:
Então a nossa integral vai ficar dividia mesmo! De até temos a parábola com sinal trocado!
Isso porque é a parte da função modular que corresponde a , sacou? Já entre , a função volta a ter a cara da parábola de antes
Então taí nossa divisão! Agora é #partiu integrar
Passo 3
Passo 4
Dividimos nossa região em duas:
Agora é só integrar e aplicar nos limites!
E a partir daqui é só resolver essas contas e partir para o abraço!
E por fim temos
Assim a integral vale
Então é isso pessoal! Terminamos!
Espero ter ajudado!
=D