No exercício 1 da lista de exercícios 4.4 fizemos a substituição de variável e calculamos a integral indefinida.
Calcule agora a integral
de duas
formas:
(1) usando a integral indefinida e substituindo os índices e
(2) reescrevendo a integral definida na variável u.
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! O problema nos lembrou que na lista 4.4 calculamos essa integral indefinida:
Usando essa substituição aqui:
E pediu para calcularmos a mesma integral, mas agora DEFINIDA
E por dois caminhos:
Primeiro utilizando o resultado da integral indefinida: com o resultado na mão, é só substituir os limites de integração dados, fazendo a função aplicada no limite superior menos ela aplicada no limite inferior.

E depois? Depois substituindo os limites de integração direto na integral por substituição em , fazendo com que nossa integral em seja definida com os limites apropriados
De qualquer forma, vou resgatar lá da lista o resultado da integral indefinida (já que vamos usar):
Note que quando aplicarmos os limites de integração (seja no final no resultado direto da integral em , ou antes na integral em com os valores correspondentes de para cada ) aquele precisa sair! Isso por porque fazemos sempre a função aplicada no limite superior (que nos daria um ) MENOS a função no limite inferior (que nos daria ), então essa constante some!

Então a ideia aqui é usar o resultado já calculado e aplicar os limites de integração e duas formas: primeiro na integral em , lá no final; e em segundo na substituição em , trocando os limites de integração de para os valores correspondentes

Mas relaxa, vou fazer passo a passo com você!
Passo 2
Primeira forma: usando o resultado da integração indefinida, aplicando os limites em no final
Nossa integral é
E usando o resultado temos o seguinte:
Agora nos resta aplicar o resultado no limite superior MENOS no limite inferior:
Beleza? E é isso!

Passo 3
Agora vamos calcular da segunda forma: na substituição feita, vamos substituir também os limites de integração em ! E integrar novamente em ! Nossa integral em é
E fazendo a substituição
Os limites ficam diferentes! Quando :
E quando :
Aí nossa integral indefinida que ora tinha ficado assim (resgatando do exercício 4.4 1h)
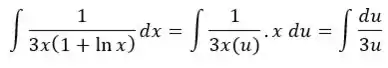
Agora vai ficar definida com os limites em correspondentes:
E agora? Agora é só integrar novamente, aplicando no final os limites:
Volta ali no finalzinho do passo 2 e repara que os resultados são IDÊNTICOS

Exatamente! Fazendo de uma ou de outra forma, o resultado é o mesmo! Então aqui é você quem vai decidir qual jeito funciona melhor para você! #vocêdecide
Agora sim! Terminamos!
Espero ter ajudado! Vamos para a próxima?