UFSC – Cálculo 1 – Lista 4.3 – Questão 4
Expresse em termos de uma integral, o deslocamento de um objeto entre os instantes de tempo e , sabendo que sua função velocidade é .
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! O problema pede para expressarmos o deslocamento de um objeto por meio de uma partícula.
Esse deslocamento deve ser feito entre os instantes e , e a velocidade é uma função do tempo
Bom, mas lá da cinemática sabemos que a variação da posição é igual a área sob o gráfico de . Como nesse exemplozinho aqui:
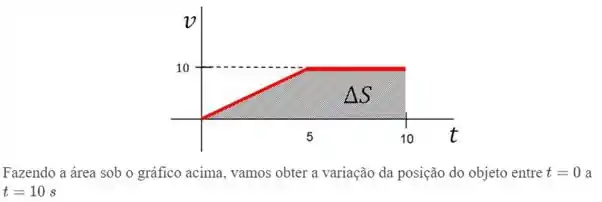
Ok?
Passo 2
Então agora se a função velocidade não é mais uma reta horizontal (como no MRU) e nem uma reta com inclinação constante (como no MRUV), mas uma curva qualquer
E agora? Como a gente pode relacionar com o deslocamento?
Da mesma forma! A área sob o gráfico de continua sendo o deslocamento! e aqui entra o cálculo! Área não é uma integral?
Então é isso! Vamos integrar a função velocidade, entre os instantes e , e assim encontrar uma expressão para o deslocamento realizado nesse intervalo de tempo
E é só isso! Essa é nossa resposta!
Espero ter ajudado! Vamos para a próxima?