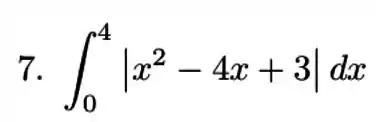
Passo 1
Para começar precisamos ver primeiro, as regiões positivas e negativas desse módulo. Para isso vamos encontrar as raízes do polinômio.
Resolvendo por soma e produto ou por qualquer outro método encontramos que as raízes são e . Aí, vamos ter que acionar aqueles conhecimentos de concavidade de parábolas agora. Lembra que, quando o valor de na parábola é positivo, a concavidade é voltada para cima, o que no nosso caso implica em
Mas e agora, como continuamos?
Passo 2
Temos que dividir nosso problema em 3 integrais
Atenção nesse sinal! Já que vimos que o modulo vai ter sinal negativo entre temos que atribuir o sinal à integral.
Passo 3
Agora vamos resolver, a primitiva vai ser a mesma nos 3 casos.
A diferença vai estar quando aplicarmos os limites de integração
Passo 4
Substituindo agora os resultados das integrais na expressão
Resposta