Lista P3 – 2020.2 – UFES – Cálculo I – Questão 2.7
Esboce a região delimitada pelas curvas dadas. Decida quando integrar em relação a ou a . Desenhe um retângulo aproximadamente típico e coloque sua altura e largura. Então, escreva a integral que dá o volume do sólido de rotação dessa área em torno das retas dadas. Em, pelo menos um dos volumes deve ser usado o método das cascas cilíndricas.
Passo 1
Faaaaala meu/minha consagradx!! Beleza?? Seguinte, vamos devagarinho aqui... parte por parte sobre o que a questão pede.
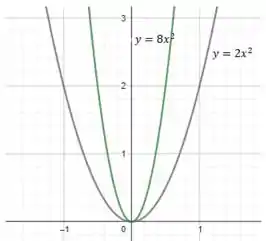
Primeiramente vamos esboçar a curva e a curva em um mesmo gráfico:
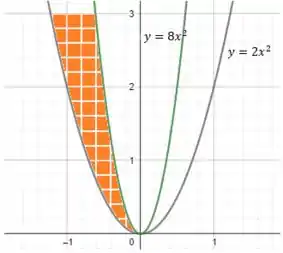
Analisando ainda mais a figura, vemos que a região delimitada entre as curvas é essa aqui ó:
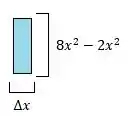
Tá... Mas e esse “retângulo aproximadamente típico” que a questão pede??
Ele não é nada mais e nada menos do que um retângulo em que a altura equivale a diferença entre as duas funções e a largura é a variação do no eixo , ou seja, . Para ficar mais fácil de entender, podemos ver:
Passo 2
Dessa forma, o volume sólido de rotação em torno do eixo , ou seja:
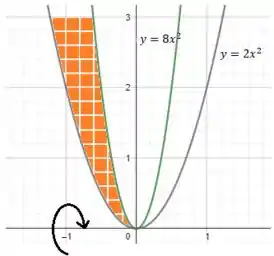
É dado pela seguinte integral:
Passo 3
Agora, em torno do eixo a gente pode usar o Método das Cascas Cilíndricas (MCC) para descobrir o volume do sólido de rotação em torno dessa reta aí. Ou seja:
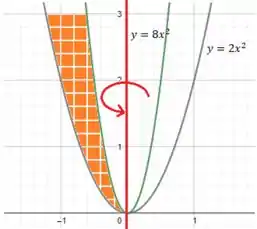
Basicamente a gente multiplica a integral por (que nem a gente calcula o perímetro de uma circunferência ;D) e dentro da integral aquele termo é pra escolher o eixo de rotação (nesse caso, bem em cima do eixo ).
Logo, resolvendo a integral, temos:
Legal ne??? Vamos para a próxima!! Valeeeeu!!
