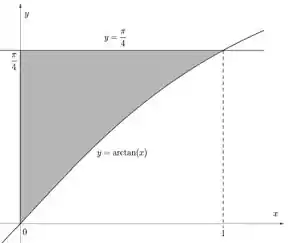
Q03) Considere a região plana definida por:
Seja o sólido de revolução obtido pela rotação de em torno do eixo
- Esboce abaixo a região plana
- Utilizando o Método de Discos, determine uma integral que forneça o volume de
- Utilizando o Método de Cascas, determine uma integral que forneça o volume de
- Calcule o volume de pelo método que preferir.
Passo 1
Pra começar e a gente entender direitinho todas as partes dessa questão, vamos começar com um esboço. Como é uma questão de volume de sólidos de revolução, o esboço não precisa ficar magnífico. Mas vamos entender que:
Significa que a região está no primeiro! Afinal, todo arco positivo tem tangente positiva! Então isso já facilita as nossas vidas. Agora, vamos focar na parte:
Oras, se a região está acima dessa curva e abaixo de uma constante, e sabemos que então já sabemos exatamente os valores de que vão entrar na integração: o valor e o valor de do ponto de interseção da curva com a constante:
E pra fechar o esboço, vamos só ver quando que a curva toca o primeiro limite de integração:
Opa, então ela parte da origem? É isso mesmo. E como a única forma de sair de e chegar em é subindo, vamos esboçar uma função contínua e crescente:
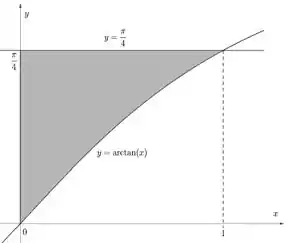
Passo 2
Show de bola, agora vamos ver o volume de . Um detalhe importante: independente do método usado, a rotação é em torno do eixo . O Método das Cascas é um método usado pra rotacionar ao redor do eixo horizontal e não o vertical! Então pra usar ele temos que inverter a função! Logo:
Ok, mas o que fazer com isso? Veja bem, quando invertemos uma função, é como se tivéssemos pegando ela e girando e depois espelhando em relação ao eixo vertical. Saca só:
Agora girando pra esquerda
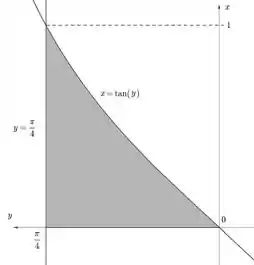
Agora espelhando:
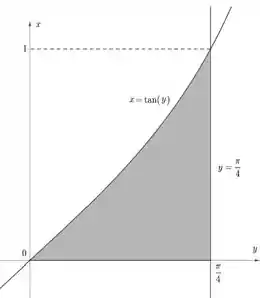
E olha só! Assim fica bem claro de ver qual integrar usar né? Se eu girar a figura acima no eixo vou estar usando o método das cascas corretamente! Seja o método:
Como a região nesse caso é simplesmente a área abaixo da curva , por esse método, temos:
Passo 3
Usando o método das cascas cilíndricas é um pouco mais tranquilo porque não precisamos inverter função nenhuma. Mas vamos precisar prestar muita atenção no seguinte. A região que queremos:
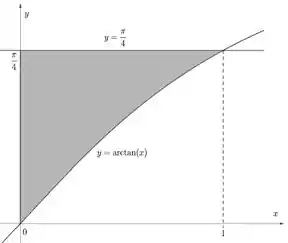
Pode ser entendida como essa área:
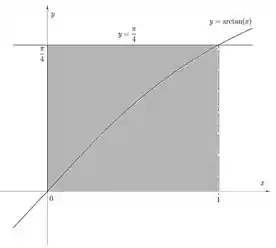
Menos essa área:
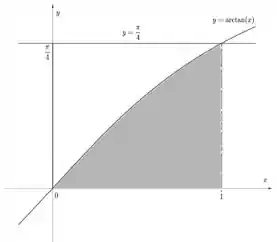
Sendo o método das cascas descrito por:
Pra primeira área, a maior, como ela é tudo abaixo da constante, indo de até , seu volume é dado por:
E pra segunda área, a menor, como ela é tudo abaixo da função, indo de até , seu volume é dado por:
O volume então vai ser:
Passo 4
Agora é com você, escolhe qual das expressões de volume quer integrar e mão na massa! A única coisa que falta é calcular o volume mesmo. Aqui pra gente fechar mais rápido a questão, como tanto faz, selecionei a mais tranquila:
Ta vendo aquele ? Será que da pra substituir? Olha, por sorte, dá sim! Afinal:
E dessa relação trigonométria maravilhosa, tiramos:
A segunda integral é super direta, então vamos calcular ela primeiro:
Já a primeira, vamos nos perguntar: qual a função que, quando eu derivo, dá ? Hmmm, pera, não era a tangente? Isso mesmo! Vamos ter então:
Tcharam! Questão finalizada :D
Resposta