UFCG – Sem Campus – Cálculo Diferencial e Integral II – Listas de Cálculo 2 – UAMat – Lista 3 – Questão 9b
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação da região sombreada em torno do eixo :
Passo 1
Eaí gente!! Vamo destruir outra questão? Vem com a gente que vai dar certo!!
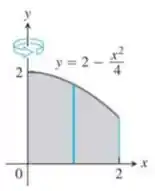
Aqui temos uma região no plano :
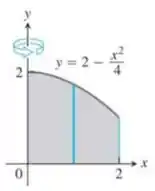
E, vamos rotacioná-la em torno do eixo , gerando o que chamamos de sólido de revolução. Para calcular o volume desse sólido, devemos usar o método da casca, que fala que:
Se rotacionarmos uma região abaixo da curva em torno do eixo , o volume do sólido obtido vale:
Show de bola! Então vamos montar essa integral para a nossa região e depois calcular o volume 😊
Passo 2
A nossa região que será rotacionada está abaixo da curva
E dentro do intervalo . Assim, lembrando que:
Temos:
Colocando as constantes para fora, ficamos com:
Usando que:
Vem:
Por fim:
Uhuuul! Até que foi rápido.Até a próxima pessoal! 😊