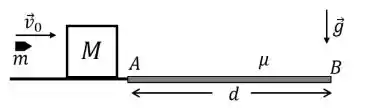
Uma bala de massa m é disparada com uma velocidade horizontal igual a v0 atingindo um bloco de massa M = 4m onde acaba alojada. Após a colisão o bloco desliza sobre uma superfície plana. Entre os pontos A e B existe atrito entre o bloco e a superfície. A distância entre os pontos A e B é igual a d. O coeficiente de atrito cinético entre o bloco e a superfície é μ. Podemos considerar que colisão é praticamente instantânea e todas as distâncias são muito maiores do que o tamanho do bloco. A resistência do ar também pode ser desconsiderada. Expresse suas respostas em termos v0, m, d, μ e g.
a) Determine a velocidade do conjunto bala+bloco imediatamente após a colisão. Justifique claramente as Leis de Conservação utilizadas.
b) Determine a velocidade do sistema após o conjunto percorrer à distância d. Justifique claramente as expressões utilizadas.
c) Determine o valor do módulo da velocidade inicial da bala, para que o conjunto bala+bloco atinja o repouso após percorrer à distância d.
Passo 1
Como a gente já sabe, numa colisão nós temos a conservação de momento linear! Então a gente tem que: . Antes temos só a bala, e depois a bala e o bloco, então temos:
Passo 2
Na letra b o bloquinho já teve um deslocamento d, então temos um Trabalho e queremos saber a velocidade no final desse deslocamento! Só usarmos o teorema do Trabalho e Energia Cinética!

Como nesse deslocamento temos a força de atrito, o trabalho vai ser realizado por ela, e vai ser negativo porque é contrário ao movimento! Então, temos:
Maneiro! Simbora!
Passo 3
Bom, agora ficou fácil! Pra o bloco atingir o repouso, ! É só a gente igualar a expressão que achamos na letra b!
Só notassoooooo!
Resposta
a)
b)
c)