Um bloco em repouso postado sobre um plano horizontal sem atrito explode em fragmentos. O primeiro se desloca para a esquerda e tem massa e o segundo move-se para a direita.
O fragmento da esquerda atinge uma região de coeficiente de atrito cinético e percorre uma distância até parar.
O fragmento da direita entra em uma região de atrito cinético e percorre uma distância até chegar ao repouso.
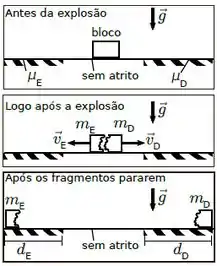
O módulo da aceleração gravitacional no local é . Determine:
- Os módulos das velocidades dos fragmentos da esquerda e da direita antes de entrarem nas regiões onde existe atrito.
- A massa do fragmento da direita.
- A variação da energia cinética do sistema entre os instantes antes e logo após a explosão.
Passo 1
Letra a)
Para achar os módulos das velocidades dos fragmentos logo antes de entrarem nas regiões com atrito nós precisamos olhar a distância que elas percorrem nessas regiões.
Vamos ver as forças que atuam sobre o bloquinho da esquerda.
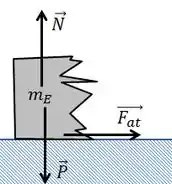
O peso e a normal se anulam e por isso são iguais.
Ao longo do eixo , a força resultante é a força de atrito, no sentido positivo.
Todo o trabalho de frear o fragmento é realizado pela força de atrito. Para o atrito cinético, ela é constante e igual a:
Assim, podemos calcular seu trabalho multiplicando pela distância percorrida. Porém, como o atrito e o deslocamento têm sentidos contrários, teremos um sinal de menos na equação, o que mostra que o atrito remove energia do movimento, parando-o.
Pelo teorema do trabalho-energia cinética, a variação da energia cinética vai ser igual ao trabalho da força de atrito, e assim:
Abrindo a fórmula da energia cinética:
Pelo enunciado:
Passo 2
O mesmo raciocínio se aplica ao fragmento da direita, o que nos dá:
Passo 3
Letra b)
Para achar a massa do fragmento da direita agora usaremos outro conceito: Momento linear.
A explosão foi interna entre os dois fragmentos, que se movem logo após a mesma sem interferências (num primeiro momento). Assim, não há forças externas e podemos afirmar que o momento linear do sistema se conserva!
Como o momento linear inicial é zero, temos:
Como os vetores tem sentidos opostos, em magnitude temos:
Passo 4
Letra c)
No instante antes da explosão, o sistema está parado, logo sua energia cinética é zero.
No instante logo após, temos:
Assim a variação da energia cinética foi:
Se toda a energia da explosão tiver sido aproveitada pra empurrar os fragmentos, poderíamos dizer que a explosão teve pelo menos uma energia de liberados.
Resposta
Letra a)
Letra b)
Letra c)