UFRJ, Sem Campus, Física 1, Roteiros de F1 - UFRJ - Roteiro 10 - Colisões, Questão 10b
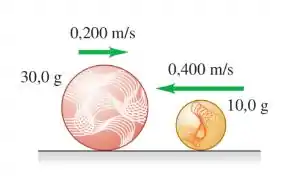
Uma bola de gude de 10,0 g desloca-se com velocidade de 0,400 m/s para a esquerda sobre uma pista horizontal sem atrito e colide frontalmente com outra bola de gude de 30,0 g que se desloca com velocidade de 0,200 m/s para a direita (Figura).
(b) Calcule a variação do momento linear (isto é, o momento linear depois da colisão menos o momento linear antes da colisão) para cada bola de gude. Compare os valores obtidos para cada bola.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos mostra a colisão entre duas bolas de gude com diferentes massas e velocidades.
A questão nos pede para calcularmos a variação do momento linear para cada bola de gude.
Para isso, temos que saber que a variação do momento linear é dada por:
Onde é o momento linear final e , o inicial.
E aí? Bora lá?
😉
Passo 2
Dessa forma, para a bola de gude A, temos
Onde:
- é a massa da bola A;
- e são as velocidades inicial e final da bola A, respectivamente;
- é a massa da bola B;
- e são as velocidades inicial e final da bola B, respectivamente;
Assim, substituindo os valores, temos:
Passo 3
Por outro lado, para a bola de gude B, temos
Onde:
Assim, substituindo os valores, temos:
Nesse sentido, podemos concluir que a variação de momento linear para ambos é a mesma. No entanto, o sentido após a colisão é contrário.
Entendeu direitinho? Responde aee ;)
