Colisão, Energia Potencial e Conservação da Energia
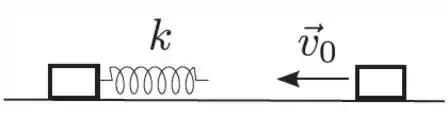
Considere dois blocos de mesma massa que podem deslizar sobre uma superfície horizontal, sem atrito. Um deles está preso a uma mola ideal de constante elástica , inicialmente relaxada, como mostrado na figura. Num referencial inercial, a velocidade inicial do bloco solto tem módulo e aponta para a esquerda, e o bloco preso à mola está em repouso. Qual o valor da compressão máxima da mola?
(a)
(b)
(c)
(d)
(e)
Passo 1
Vamos considerar o sistema blocos+mola.
Quando o bloco da direita bater na mola, ao mesmo tempo que a mola vai ser comprimida, o sistema todo vai começar a se mover pra esquerda.
O atrito é desprezível, a colisão é feita sem forças externas atuando, então podemos aplicar a conservação do momento linear:
e sendo, respectivamente, os momentos lineares do sistema antes e depois da colisão.
Passo 2
Todo o movimento vai ser pra esquerda, então pra não ter que ficar botando sinal negativo, vamos considerar a velocidade pra esquerda como sendo positiva. Assim, o momento linear total antes da colisão é:
Passo 3
E depois da colisão, o sistema todo está se movendo junto, com massa (a mola é ideal então tem massa desprezível) e velocidade que podemos chamar de . Ou seja,
Passo 4
Voltando à conservação do momento linear:
Passo 5
Como a colisão aconteceu sem atuação de forças dissipativas, podemos usar também a conservação da energia mecânica! Vamos considerar o movimento do momento inicial (da figura) até o momento em que a mola está comprimida na sua compressão máxima .
No começo só tem a energia cinética do bloco da direita, e depois tem a energia cinética do sistema todo, mais a energia potencial elástica por causa da compressão da mola.
Passo 6
Sendo a energia cinética e a energia potencial elástica, a equação de conservação da energia mecânica vai ser:
Lembrando que chamamos de a compressão máxima da mola:
Passo 7
Multiplicando tudo por 2:
Resposta
Alternativa (c)