Uma esfera de massa é lançada em um trilho unidimensional de atrito desprezível com velocidade ao encontro de uma segunda esfera lançada simultaneamente de massa desconhecida com velocidade . As esferas colidem elasticamente e durante a colisão a primeira esfera sofre uma força dada pelo gráfico abaixo.
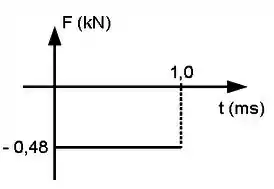
(b) Determine a velocidade imediatamente depois da colisão da primeira esfera.
(c) Determine a velocidade imediatamente depois da colisão da segunda esfera e o valor de sua massa.
Passo 1
(b)Analisar o que acontece com a esfera
Em uma colisão elástica, duas coisas podem acontecer, dá uma olhada:
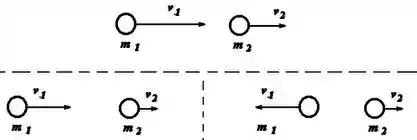
Independente de qual vai acontecer, a velocidade da esfera vai mudar, beleza? Então, mesmo que o momento linear do sistema se conserve, pra a bolinha isolada não vai ser o caso!
Passo 2
Analisar a fórmula do impulso
Vamos lembrar a fórmula do impulso?
Tá, e daí? O que eu faço com isso? Bem, pra essa fórmula fazer algum sentido pra gente, temos que lembrar do gráfico que o enunciado nos deu de presente: um gráfico de força por tempo! Na fórmula do impulso tem tanto força quanto tempo! Então, a forma vetorial, vamos ter:
Passo 3
Calcular a velocidade com a expressão encontrada
É galera, agora ta no papo. Já sabemos como explicitar a velocidade final em função de valores conhecidos, então agora é só substituir e fazer contas!
Passo 4
Usar a troca de velocidade relativas
Temos de velocidades: as iniciais, dados do problema, e a velocidade final da bolinha . Pra achar então a velocidade que falta, temos todos os dados que a gente precisa, não é mesmo? Então vamos partir pras contas e achar o que falta. Usando a troca de velocidades relativas:
Passo 5
Fazer a conservação do momento linear pro sistema
Cansado? Calma, esse é o último passo! O que falta agora é achar a massa da segunda esfera. Até agora não usamos a clássica conservação do momento linear pra nada não é mesmo? Vamos usar agora então!
Chega de rearranjar! Vamos pros números que é o que importa:
Resposta
b)
c)