Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Conservação do Momento Linear

Ver Teoria
Exercício 124123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 33a

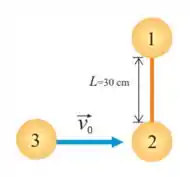
33. Um haltere formado por dois discos 1 e 2 iguais de massa m unidos por uma barra rígida de massa desprezível e comprimento L = 30   c m repousa sobre uma mesa de ar horizontal. Um terceiro disco 3 de mesma massa m , desloca-se com atrito desprezível e velocidade v 0 = 3   m / s sobre a mesa, perpendicularmente ao haltere, e colide frontalmente com o disco 2 , ficando colado a ele.

(a) Determine o vetor posição do centro de massa em função do tempo.

Passo 1

Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍

Nesse problema temos dois discos de massa m presas por uma barra de massa desprezível e comprimento L = 30   c m . Um terceiro disco viaja com velocidade v 0 = 3   m / s em direção ao disco 2 que ao colidirem, se grudam e o sistema inteiro começa a se mover.

Com isso queremos obter a posição do vetor centro de massa do sistema em função do tempo!

E aí, parece complicado? 👀

Nesse caso, podemos aplicar a ideia de conservação do momento linear e dizer que o momento linear no início do problema é igual ao momento linear no fim do problema, ou seja...

P i = P f

Que por sua vez, o momento linear de um sistema é dado por

P = m v

Sacou? Bora começar! 😉

Passo 2

Inicialmente o disco 3 está em movimento e os discos 1 e 2 estão parados, portanto o momento linear inicial é dado por

P i = m v 0 + 2 m 0

P i = m v 0

Já após a colisão o momento linear será dado por

P f = 3 m v c m

Igualando as duas equações, chegamos em

P i = P f

m v 0 = 3 m v c m

Simplificando e isolando v c m , vamos obter

v c m = m v 0 3 m

v c m = v 0 3 = 3 3

v c m = 1   m / s  

A partir do vetor velocidade, podemos entender como o sistema se move com o tempo, ou seja, como o vetor posição do centro de massa R → varia em t ...

Portanto no eixo x o vetor posição pode ser obtido como

R → x = 1 t   i ^

Tranquilo até aqui? 😬

Passo 3

Porém quando o disco 3 gruda no disco 2 , há uma mudança no centro de massa do conjunto barra-discos...

Essa mudança de centro de massa provoca uma variação de R → em y , ou seja

y c m = m 1 y 1 + m 2 y 2 + m 3 y 3 m 1 + m 2 + m 3

Sabemos que m 1 = m 2 = m 3 = m .

y 1 está a uma altura L = 0,3   m da referência e y 2 e y 3 estão a uma altura 0 .

y c m = m 0,3 + m 0 + m 0 m + m + m

y c m = 0,3 m 3 m

y c m = 0,1

Assim o vetor R → do centro de massa é dado após a colisão por

R → c m = 1 t   i ^ + 0,1   j ^

E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí

Resposta

R → c m = 1 t   i ^ + 0,1   j ^

Exercícios de Livros Relacionados

Dois veículos espaciais em órbita estão acoplados. A massa de um deles é de 1000 Kg e a do outro de 2000 Kg. Para separá-los, é denotada entre os dois uma pequena carga explosiva, que comunica uma ene
Vários pesquisadores em ensino de física alegam que parte da origem das concepções alternativas entre os estudantes são os efeitos especiais que eles veem em desenhos animados e em filmes. Usando a co
Uma espaçonave é separada em duas partes pela detonação dos rebites explosivos que as mantêm unidas. As massas das partes são 1200k g e 1800k g ; o módulo do impulso que a explosão dos rebites exerce
"Relativamente" é uma palavra importante. Na Fig. 9-72, o bloco E de massa m e =1,00k g e o bloco D de massa m D=0,500k g são mantidos no lugar com uma mola comprimida entre os dois blocos . Quando os
Um certo núcleo radioativo (pai) se transforma em um núcleo diferente (filho) emitindo um elétron e um neutrino. O núcleo pai estava em repouso na origem de um sistema de coordenadas x y . O elétron s