Uma partícula de massa se move com velocidade e aproxima-se de outra partícula de mesma massa que está parada em uma superfície sem atrito. As duas partículas colidem obliquamente. Logo após a colisão a primeira partícula passa a se mover com uma velocidade de módulo fazendo um ângulo de acima da direção de seu movimento antes da colisão. A segunda partícula logo após a colisão passa se mover com uma velocidade com módulo fazendo um ângulo de abaixo da direção inicial que tinha a primeira partícula antes da colisão.
(b) Determine os módulos das velocidades das partículas e logo após a colisão.
(c) Determine se a colisão foi elástica ou inelástica.
Passo 1
(b)Analisar o que acontece após a colisão
Enunciado sem figura é mais difícil não é? Mas relaxa, dá uma olhada nesse esquema:
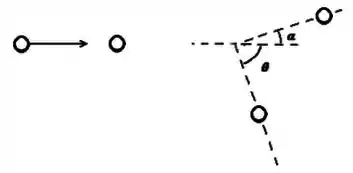
Nesse esquema a gente vê o antes e o depois da colisão! Os ângulos, pelo enunciado, são:
Tá, mas o que eu faço com essa informação? Bem, veja: se as duas velocidades finais são anguladas, podemos decompor os vetores e em componentes verticais e horizontais e considerar a conservação do momento linear nas duas direções!
Passo 2
Conservação do momento linear no eixo horizontal
Vamos começar com o eixo horizontal, beleza? Saca só:
A partícula estava inicialmente em repouso, lembra? E as partículas tinham massas iguais também! Agora a fórmula fica bem mais simples:
Reescrevendo as velocidades horizontais, ficamos com:
Passo 3
Conservação do momento linear no eixo vertical
Pro eixo vertical, podemos fazer a mesma coisa, então vamos ter:
Ué, mas esse sinal de ““, o que ele tá fazendo aí? Calma, pra entender ele é só lembrar que a partícula está “descendo” enquanto a partícula está subindo, mesmo que ambas estejam indo pra direita. Reescrevendo, então, as velocidades horizontais, ficamos com:
Passo 4
Resolver o sistema de equações
Tanta conta até agora e cadê a resposta? Calma, ela vai aparecer. Vamos rever o que conseguimos até agora:
Epa, reconhece isso? É um sistema de equações com duas equações e dus incógnitas. Agora sim conseguimos achar as velocidades finais! Pra resolver esse sistema de equações, vamos primeiro multiplicar a equação por . Vamos ter:
E depois, vamos somar as equações e :
Aee, uma velocidade já foi! Agora falta a outra. Substituindo o resultado em , vamos ficar com:
Passo 5
(c)Determinar o tipo de colisão
Seja a colisão elástica ou inelástica, vamos ter de qualquer modo a conservação do momento linear, não é mesmo? Então qual é o critério de desempate? O que fizemos até agora não nos permite classificar o tipo de colisão!
O critério de desempate vai ser a energia cinética! Se ela se conservar, a colisão será elástica. Se não se conservar, será inelástica. Vamos calcular então?
Como a energia cinética vai se conservar! A colisão então será elástica!
Resposta
b)
c) Colisão elástica