Um pêndulo de comprimento e massa é solto do repouso a um ângulo de da vertical. Quando o pêndulo atinge a posição vertical, ele atinge uma caixa de massa , em repouso sobre uma mesa sem atrito. A mesa tem uma altura de , conforme figura. Usar, se necessário, as aproximações e .
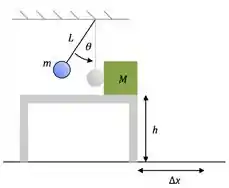
- Calcule a velocidade do pêndulo na posição vertical antes de atingir a caixa.
- Calcule a velocidade do pêndulo e da caixa logo após a colisão perfeitamente elástica.
- Determine o impulso sofrido pela caixa durante a colisão.
- Um carro de altura desprezível e massa é colocado na posição onde a caixa deveria cair no solo. A caixa cai sobre o carro e eles se grudam em uma colisão perfeitamente inelástica. Calcule a velocidade horizontal do carro logo após a caixa cair sobre ele.
Passo 1
- Conservando a energia, teremos:
- Como a colisão é perfeitamente elástica, podemos conservar o momento linear e a energia cinética. Assim:
- Sabendo que:
- Como a colisão é perfeitamente inelástica, após a colisão, os corpos caminham juntos. Sabendo que não há forças externas atuando no sistema, podemos conservar o momento linear, assim:
Sendo o comprimento do pêndulo e a componente vertical no momento em que o pêndulo inicia o movimento, podemos calcular como:
Logo,
Passo 2
Substituindo os dados, teremos:
Isolando em e substituindo em , teremos:
Resolvendo a equação encontraremos:
Logo,
Passo 3
Para a caixa, teremos:
Passo 4
Resposta
Exercícios de Livros Relacionados
Dois veículos espaciais em órbita estão acoplados. A massa de um deles é de 1000 Kg e a do outro de 2000 Kg. Para separá-los, é denotada entre os dois uma pequena carga explosiva, que comunica uma ene
Vários pesquisadores em ensino de física alegam que parte da origem das concepções alternativas entre os estudantes são os efeitos especiais que eles veem em desenhos animados e em filmes. Usando a co
Uma espaçonave é separada em duas partes pela detonação dos rebites explosivos que as mantêm unidas. As massas das partes são 1200k g e 1800k g ; o módulo do impulso que a explosão dos rebites exerce
"Relativamente" é uma palavra importante. Na Fig. 9-72, o bloco E de massa m e =1,00k g e o bloco D de massa m D=0,500k g são mantidos no lugar com uma mola comprimida entre os dois blocos . Quando os
Um certo núcleo radioativo (pai) se transforma em um núcleo diferente (filho) emitindo um elétron e um neutrino. O núcleo pai estava em repouso na origem de um sistema de coordenadas x y . O elétron s