USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 1 - Polinômio de Taylor e Curvas Planas, Questão 2.2a
Esboce e parametrize cada conjunto como uma curva:
Passo 1
Oiie, tudo bem?
Nós temos que esboçar e parametrizar os conjuntos indicados em cada alternativa, nesta em particular temos que
Temos que a equação indicada é bastante conhecida! E, algumas desigualdades que limitam um pedaço que estamos interessados! Consegue identificar? Saca só!
Passo 2
A equação
é a equação de uma circunferência de raio , a parametrização deste tipo de curva é bastante conhecida, temos que
uma circunferência completa tem no intervalo , devido a presença das desigualdades em iremos precisar verificar esses limites! Saca só!
Passo 3
Usando a nossa parametrização temos que a desigualdade se torna
de forma que
Isso dá um limite superior para o valor de equivalente à
Da mesma forma temos que a desigualdade , nos leva ao limite
Talvez você precise dar uma olhada no gráfico para compreender a escolha dos ângulos! Portanto, a parametrização é dada por
em que
A região descrita pelo conjunto e portanto a curva descrita é a seguinte
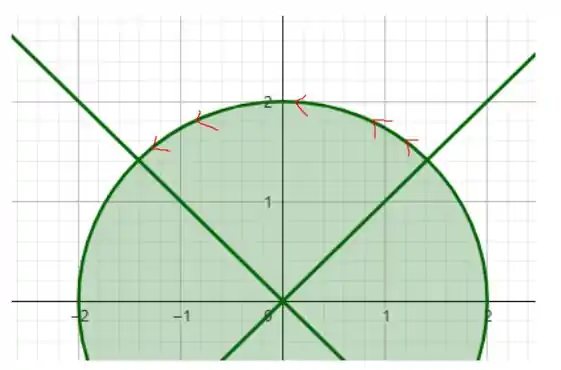
Resposta
em que