USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 1 - Polinômio de Taylor e Curvas Planas, Questão 2.2c
Esboce e parametrize cada conjunto como uma curva:
Passo 1
Oiie, tudo bem?
Nós temos que esboçar e parametrizar os conjuntos indicados em cada alternativa, nesta em particular temos que
Esta equação é uma função bem conhecida, consegue reconhecer? A sua parametrização requer passarmos por um pequeno truque, vou mostrar no próximo passo! A desigualdade apenas nos indica que pedaço da curva iremos considerar! Saca só!
Passo 2
A seguinte equação
é a equação de uma hipérbole com o centro deslocado para a posição . Mas como parametrizamos isso? De maneira bem similar a circunferência, mas para enxergamos isso, vamos reescrever um pouco essa equação, temos que
se chamarmos e , obtemos a equação de uma hipérbole centrada na origem
convenientemente vou escrever esta expressão da forma
Isso irá nos ajudar muito, pois agora temos uma identidade trigonométrica que parametriza a nossa curva muito bem! Saca só!
Passo 3
Se lembrarmos que , podemos notar que usando
e
podemos garantir uma parametrização! Lembrando as variáveis originais, temos que
e
e, portanto, a parametrização é
e como temos que nunca é zero, precisamos apenas tomar a curva que está abaixo do eixo , representada por
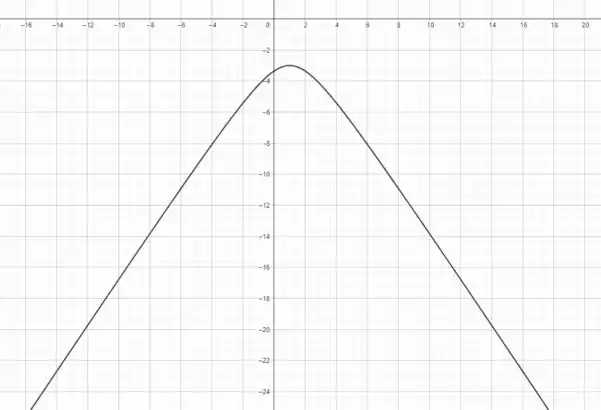
A questão foi isso! Te vejo na próxima! Tchau Tchau!