USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 1 -Polinômio de Taylor e Curvas Planas, Questão 2.10a
Considere a curva plana dada por
Esboce a imagem da curva e o sentido do percurso. Sugestão: tente calcular em alguns pontos e ver se consegue visualizar a curva e o sentido do percurso, depois cheque usando algum aplicativo: desmos ou wolframalpha ou outro. O nome dessa curva é “caridióide” - você vai entender a razão!
Passo 1
Eaew, tudo certinho?
Essa questão é bastante direta, nos foi dada a seguinte curva
e, precisamos nesta alternativa
Esboce a imagem da curva e o sentido do percurso. Sugestão: tente calcular em alguns pontos e ver se consegue visualizar a curva e o sentido do percurso, depois cheque usando algum aplicativo: desmos ou wolframalpha ou outro. O nome dessa curva é “caridióide” - você vai entender a razão!
ou seja, vamos jogar valores para dentro do intervalo e fazer um esboço do gráfico! Em particular, eu vou indicar os pontos no gráfico feito usando o geogebra por uma questão de apresentação, mas tente desenhar ligando os pontos como fazíamos em pré-cálculo, tudo bem? Vamos lá!
Passo 2
Vamos tentar alguns valores de , em particular, vamos tentar os valores , saca só o que obtemos
ou seja, um ponto com coordenadas , vamos continuar substituindo
ou seja, subimos um pouco na coordenada e fomos para a direita na coordenada . Mas isso ainda não é o suficiente, vamos continuar
continuamos subindo em e indo para a direita em . Agora para
Ora, o valor de começou a diminuir e o valor de continua aumentando! Ou seja, isso começa a indicar um sentido horário para o movimento da curva! Vamos colocar os valores que faltam e verificar
e, também
e, por último
o plot é da forma
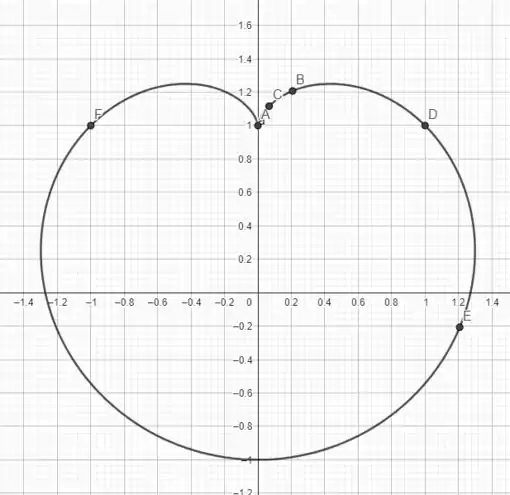
Notou porque se chama cardióide? Perceba de A à F temos os pontos que calculamos, G é para e ele coincide com . Portanto, o movimento é no sentido antihorário! A primeira alternativa foi essa! Te vejo na próxima!
Resposta
Ao longo dos passos!