USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 1 - Polinômio de Taylor e Curvas Planas, Questão 2.2d
Esboce e parametrize cada conjunto como uma curva:
sendo e a reta .
Passo 1
Oiie, tudo bem?
Nós temos que esboçar e parametrizar os conjuntos indicados em cada alternativa, nesta em particular temos que
sendo e a reta .
Aqui temos a forma reduzida de uma equação conhecida! Note que a função indica a distância entre duas grandezas, aqui em particular, temos que a distância de qualquer par coordenado à uma reta é a mesma distância de qualquer par coordenado de um ponto . Consegue visualizar que figura geométrica tem essas características?
Passo 2
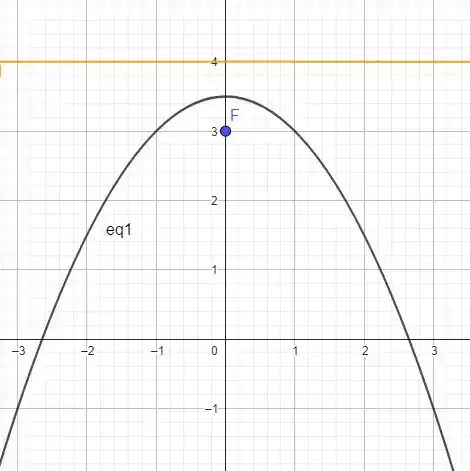
A figura desejada é uma parábola, se identificarmos que é a reta diretriz (uma reta horizontal) e o ponto é o seu foco! Já que a distância de qualquer ponto da parábola ao foco é igual a distância de qualquer par coordenado com a diretriz da seguinte forma
Como temos que a diretriz é , e o Foco é , usando um ponto cartesiano arbitrário, e a definição de distância, temos que a equação da parábola pode ser obtida igualando
à
note que na segunda distância escolhi um ponto para representar uma reta . Vamos agora igualar as duas equações!
Passo 3
Igualando as equações temos que
elevando ambos os lados ao quadrado, temos que
expandindo os quadrados, obtemos
simplificando alguns termos, obtemos que
que pode ser representada como
A questão foi isso! Te vejo na próxima! Tchau Tchau!