USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 1 - Polinômio de Taylor e Curvas Planas, Questão 2.2b
Esboce e parametrize cada conjunto como uma curva:
Passo 1
Oiie, tudo bem?
Nós temos que esboçar e parametrizar os conjuntos indicados em cada alternativa, nesta em particular temos que
Esta equação não é uma das conhecidas, mas é possível fazer uma parametrização escolhendo uma das variáveis como base! E, algumas desigualdades que limitam um pedaço que estamos interessados! Saca só!
Passo 2
Podemos tornar a variável em um parâmetro , ou seja, se temos uma equação da forma
a nossa parametrização se torna
mas, quais são os limites de ? Isso será dado pelas desigualdades apresentadas no conjunto . Vamos lá!
Passo 3
Temos que como , necessariamente, , e como temos que
podemos garantir a desigualdade
ou simplesmente
lembre que ao dividir por um número negativo você deve inverter a desigualdade. Sendo assim a parametrização se torna
em que
Podendo ser representada como
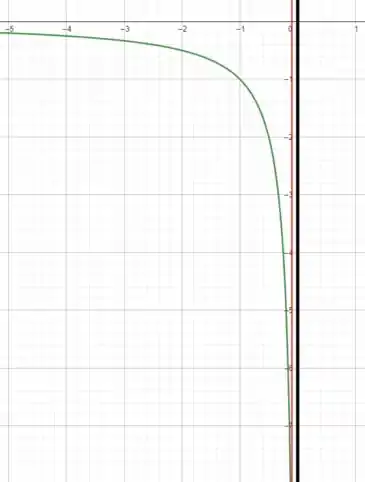
mas a limitação faz com que consideremos apenas o intervalo
Note que a curva tende a enquanto . A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
em que