USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 1 -Polinômio de Taylor e Curvas Planas, Questão 2.10b
Considere a curva plana dada por
O ponto mais à direita da curva é…
Passo 1
Eaew, tudo certinho?
Essa questão é bastante direta, nos foi dada a seguinte curva
e, precisamos nesta alternativa determinar
O ponto mais à direita da curva é…
Vamos usar alguns resultados da alternativa anterior! Temos o plot dado por
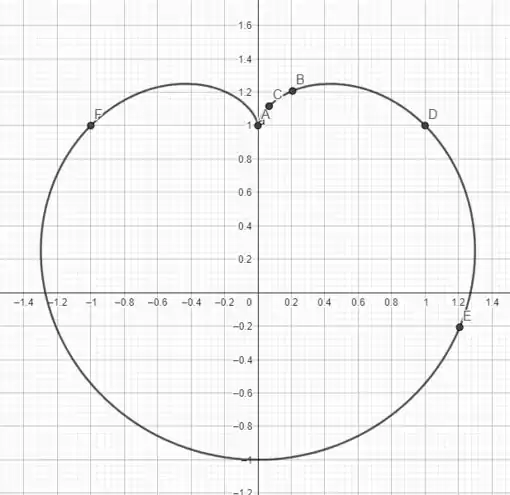
o ponto mais à direita será algo entre o ponto e que são para e . O ponto mais à direita será dado por que zera a componente horizontal da derivada da função, portanto, vamos calcular a derivada desta curva em termos do parâmetro ! Vem comigo!
Passo 2
Precisamos calcular
distribuindo em ambos os componentes, temos que
usando a regra do produto, da cadeia e algumas derivadas conhecidas, temos que
Agora lembre-se que a derivada é geometricamente relacionada a inclinação da reta tangente a curva! No ponto que desejamos, o maior ponto à direita, temos que a reta é vertical, ou seja, sua componente horizontal é nula! Ou seja?
Passo 3
… Ou seja, temos encontrar um valor de entre e , tal que
usando que , obtemos simplesmente
para facilitar nossa vida, vamos chamar , de forma que obtemos o seguinte polinômio de segundo grau
aplicando Bhaskara temos que
ou duas possibilidades
e
ou seja, como , vamos procurar valores de tal que
ou
Vamos lá!
Passo 4
Temos que
quando , portanto, não existe solução no intervalo que indiquei no começo desta alternativa! No entanto, temos que
quando que está no intervalo desejado! Portanto, o valor mais a direita é
Aí está mais uma alternativa! Te vejo na próxima!