USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 1, Questão 2.1g
Desenhe as imagens das seguintes curvas, indicando o sentido de percurso:
g. ;
Passo 1
Eaew, belezinha?
Temos desenhar a seguinte curva parametrizada:
Vamos escolher valores de e avaliar os valores de e , então poderemos construir um gráfico de em função de , ou vice versa. Vamos lá!
Passo 2
Primeiro vamos construir a tabela cujas colunas terão os valores de e os valores de e :
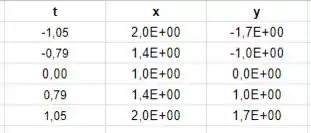
Passo 3
Também podemos escrever y em função de x, para isso fazemos a seguinte manipulação utilizando relações trigonométricas
substituindo em y
.
Passo 4
Assim, podemos construir o gráfico indicando o sentido do percurso da curva , como colocamos poucos pontos o comportamento curvilíneo da curva não fica tão evidente:
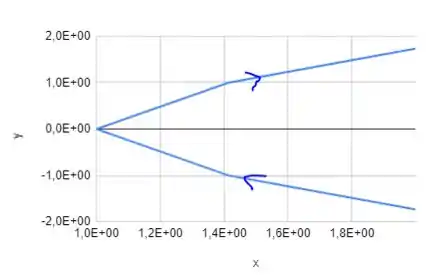
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
No decorrer da questão.
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica