USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 1 - Polinômio de Taylor e Curvas Planas, Questão 2.2e
Esboce e parametrize cada conjunto como uma curva:
sendo e .
Passo 1
Oiie, tudo bem?
Nós temos que esboçar e parametrizar os conjuntos indicados em cada alternativa, nesta em particular temos que
sendo e .
Aqui temos a forma reduzida de uma equação conhecida! Note que a função indica a distância entre duas grandezas, aqui em particular, temos que a distância de qualquer par coordenado a um ponto somada a distância do mesmo par coordenado à um ponto tem módulo igual a . Consegue visualizar de qual objeto estamos falando?
Passo 2
A figura desejada é uma elipse com focos em e , em que podemos identificar a forma reduzida no formato
ou seja, podemos garantir que , e portanto, o semi-eixo menor é dado por . Para escrever a equação no formato que conhecemos podemos utilizar a definição de distância como
e, então, aplicar a nossa definição! Saca só!
Passo 3
Usando a definição de distância temos que
que pode ser simplificado para
elevando ambos os lados ao quadrado, temos que
expandindo os quadrados, e simplificando, temos que
elevando ao quadrado novamente
expandindo o quadrado e simplificando novamente
reorganizando e simplificando, temos que
ou simplesmente
Uff… podemos visualizar nossa elipse como
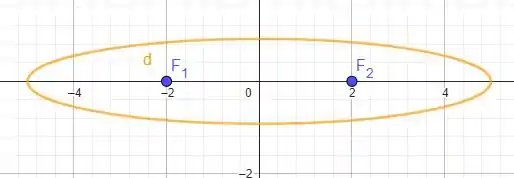
A questão foi isso! Te vejo na próxima! Tchau Tchau!