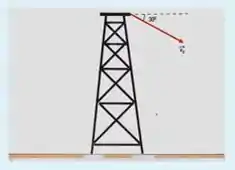
Do alto de uma torre de de altura, uma esfera e lançada com velocidade de numa direção que forma com a horizontal, para baixo. Desconsiderando a resistência do ar e admitindo , , qual o instante e a distância que a esfera atinge o solo, respectivamente?

Escolha uma opção:

1. e
2. e
3. e
4. e
5. e
6. e
7. e

Vamos agora identificar as quantidades iniciais: o módulo da velocidade é , e agora precisamos identificar no desenho quem são as componentes vertical e horizontal em relação ao ângulo dado:

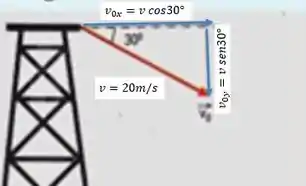
O módulo da velocidade é o tamanho do vetor em vermelho no desenho, então podemos fazer um triângulo retângulo com as duas componentes: e . O cateto oposto ao ângulo dado é a componente vertical, sendo assim podemos escrever essa componente em função do ângulo dado:

Aqui preciso fazer uma observação: essa velocidade aponta no sentido negativo! A esfera é lançada pra baixo, então . E isso vai aparecer na equação de movimento mais pra frente! Aqui só escrevi o módulo da componente, ok?

E o cateto adjacente está relacionado com a componente horizontal. Esse cateto pode ser reescrito em função do cosseno:

Beleza até aqui?

Então essas são nossas velocidades iniciais nas direções e . A posição inicial vertical é a altura da torre, então:

E a horizontal? Bom, como queremos depois encontrar o alcance, vou supor que a posição horizontal inicial é zero, pra facilitar nossa vida:

Lembrando que na direção horizontal não temos aceleração! E que na direção temos a gravidade! (e ela aponta para baixo!)

Agora vamos escrever as equações de movimento para as duas direções!

Na horizontal temos só a equação de posição em função do tempo, vamos usar a velocidade inicial e a posição inicial que indiquei ali no passo anterior:

Lembrando que , pois no MRU a velocidade não muda com o passar do tempo =)

E para o movimento vertical temos também a equação da posição, usando a posição e a velocidade inicial:

Aqui já coloquei que a gravidade e a velocidade inicial apontam pra baixo! A gravidade sempre aponta para baixo! Já a velocidade inicial pode ser positiva (quando se arremessa a esfera pra cima) ou negativa (que é o nosso caso, ela é jogava verticalmente pra baixo!) , dependendo do problema! Daí você precisa ficar atento nisso, ok?

Agora vamos substituir os valores iniciais:

Pronto! Temos as equações de movimento que irão nos dar a posição em função do tempo desse arremesso!

Agora vamos calcular o que se pede!

Para calcular o instante que a bola encosta no chão podemos usar a equação de , pois quando a bola chega no chão e queremos saber o instante em que isso acontece. Então precisamos substituir por na equação do passo anterior e achar o valor de :

Essa é uma equação de segunda ordem e vamos aplicar a fórmula de Bhaskara pra resolver para . Vamos começar dividindo tudo por , assim vamos ter o coeficiente de igual a , o que facilita muito nossa vida:

Os coeficientes são:

Lembrando da fórmula...

Aqui temos duas soluções, mas fisicamente a única possível é quando o tempo é positivo:

Assim o tempo que a bola leva para chegar ao chão é .

Tranquilo até aqui?

Agora para achar o alcance horizontal da bola, podemos usar a equação de movimento horizontal! Isso porque quando a bola chega no chão, ela atingiu sua maior distância horizontal e o movimento acaba! Então resgatando a equação lá do passo 3 temos:

E agora queremos saber essa posição quando :

Assim o instante que a bola toca o chão é e o alcance horizontal é , alternativa correta é a (g).

Ufa! Terminamos!

Bora pra próxima?