UFF, Sem Campus, Física 1, Listas Cursos de Verão 2023 - Lista 2 - Queda Livre e Vetores, Questão 5.
5) Uma partícula sobre três deslocamentos sucessivos em um plano da seguinte forma: para sudoeste, para leste e para a direção ao norte de leste. Escolhendo o eixo orientado para leste e o eixo orientado para norte, determine
a) As componentes de cada deslocamento,
b) As componentes do deslocamento resultante,
c) o módulo e a direção do deslocamento resultante,
d) o deslocamento requirido para trazer a partícula retornar ao ponto de partida
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema temos uma partícula que se movimenta no plano e nosso objetivo é determinar as componentes de cada deslocamento, do deslocamento resultante, o modulo e direção do deslocamento resultante e o deslocamento necessário para trazer a partícula para o ponto inicial.
E aí, preparado? 👀
Primeiro a partícula sai da origem e anda para sudoeste.
Depois anda para leste.
E por último, anda para a direção ao norte de leste.
Passo 2
Se escrevermos os vetores deslocamento para , e ...
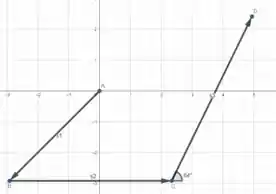
Sudoeste fica a do eixo , cortando o quadrante ao meio. Portanto, lembrando do quadrado e sua diagonal, temos que a diagonal do quadrado é dado por
Se a diagonal é o modulo do vetor, então ...
Assim, o vetor é dado por
Para o vetor , o movimento é em direção a leste, ou seja, em direção a positivo.
Portanto, podemos escrever como
E por fim, o vetor é dado por fazendo um ângulo de com a horizontal.
Tranquilo até aqui? 😁
Passo 3
O vetor deslocamento resultante é dado pela soma dos vetores , e .
Calculando o módulo e a direção de
Para obter a direção, vamos usar a regra da tangente em relação ao eixo positivo.
E por fim, para voltarmos à origem do sistema, basta aplicarmos
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
a) , e
b)
c) ,
d)