Uma jogadora de futebol chuta uma bola em uma direção de com o plano do campo. Depois de a bola toca o campo novamente. Qual é o alcance da bola? Desconsidere a resistência do ar, considere , .
Passo 1
Fala galera, tudo bem?! Vamos resolver essa aqui juntos?
Primeiro a gente tem que identificar que essa questão é uma composição de movimentos: MRU na horizontal e MRUV na vertical. Mas como assim?
Bom, a horizontal não fala que temos aceleração, então é porque não temos mesmo! E um movimento sem aceleração é um movimento retilíneo uniforme! A velocidade inicial vai ser a componente horizontal do vetor velocidade e o alcance é a distância percorrida durante o tempo de voo desse bichinho aí!
Já na vertical temos a gravidade, que aponta sempre para baixo, então temos um movimento acelerado. A bola vai subir, atingir uma altura máxima e voltar para o chão. O tempo que ela leva fazendo esse movimento é o tempo de voo, beleza?
A ideia para resolver essa questão é identificar que o tempo de voo (que nos foi dado) é o mesmo tempo que a bola leva para subir e descer, mas também o tempo que ela tem para se deslocar horizontalmente!
E, com as equações de movimento vertical e horizontal, achar o alcance da bola!
Calma que vou fazer passo a passo contigo! Segura minha mão e vem comigo!

Passo 2
Vamos lembrar qual é a equação da posição em função do tempo no MRU:
Quando temos que a distância horizontal percorrida é igual ao alcance da bola , e admitindo que a bola parta da origem :
No nosso caso, a velocidade vai ser a componente horizontal do vetor velocidade. Para achar ela em função do ângulo dado, dá uma olhada na trajetória dessa bolinha:
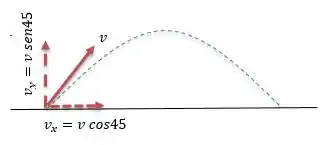
E a gente pode desenhar um triângulo retângulo com as componentes e o módulo do vetor:
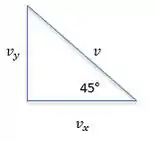
A componente horizontal é o cateto adjacente do triângulo que se forma com , então ela vai com o cosseno do ângulo. Já a componente vertical é o cateto oposto, então ela vai com o seno.
Assim o alcance da bola é:
Sabemos o tempo, mas não sabemos a velocidade inicial.

Tudo bem até aqui?
Passo 3
Agora vamos olhar para o movimento na vertical e tentar achar outra equação que nos ajude para achar esse alcance aí!
Sabemos que o tempo de voo é de , então sabemos que o tempo que a bolinha sai do chão, ou seja , até chegar de novo no chão , é . Então temos duas informações de posição e tempo! Da equação de posição pro MRUV temos o seguinte:
A aceleração da gravidade sempre aponta para baixo, por isso o sinal de ali na equação. A velocidade inicial está relacionada com o cosseno, como falei ali no passo anterior. Então temos quase todos os valores, menos a.... velocidade! Isso mesmo! Daqui a gente consegue determinar qual é o módulo da velocidade! E daí com esse valor, a gente volta pra equação do alcance e acha ele! Beleza? Vamos lá?
Substituindo os valores temos:
E daí a equação fica:
Passo 4
Agora com o valor da velocidade, é só resgatar do passo 2 a expressão para o alcance e substituir os valores:
Pronto! O alcance da bola foi de
Beleuza?
