USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 14b
Um trem parte de uma estação com aceleração constante de Um passageiro chega à estação segundos depois de o trem ter passado pelo mesmo ponto da plataforma. Qual é a menor velocidade constante que o passageiro deve correr para pegar o trem?
Resolva o problema de duas maneiras:
b) graficamente;
Passo 1
E aí gente bonita, como vocês estão?
Nessa questão temos um passageiro bem atrasadinho que chega na estação depois que o trem passou por ela. O enunciado nos fala que o trem parte da plataforma em repouso com uma aceleração constante de .
Precisamos calcular a menor velocidade constante que o passageiro deve ter para alcançar o trem.
Para fazer isso, vamos utilizar as equações horárias da cinemática envolvendo os dois tipos de movimento realizados pelos corpos: MRUV e MRU.
No MRU temos as seguintes equações horárias:
Já para o MRU, temos:
Massa!
Porém, o enunciado nos pede para fazer isso graficamente. Então, a ideia é usarmos as equações horárias da posição para esboçar o gráfico, e analisar qual a velocidade mínima pra que as duas curvas de posição (do trem e do passageiro) se cruzem.
Vem com a gente que vai ficar mais claro 😊
Passo 2
Vamos começar escrevendo a equação horária da posição do trem, que como possui aceleração constante, realiza um movimento do tipo MRUV. Ou seja:
O instante inicial que iremos considerar é quando o trem parte da estação. Assim:
Logo:
Essa é a equação de uma parábola com ponto de mínimo e raiz dupla em também.
Podemos esboçar essa curva, como:
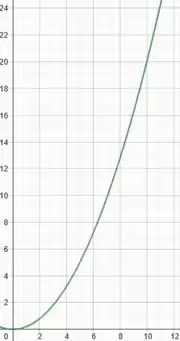
Massa!
Passo 3
Vamos pensar agora na curva que a posição do passageiro vai descrever.
Primeiramente, como ele só chega à plataforma após o trem partir, a sua curva deve começar em .
Além disso, sua velocidade é constante, então:
Quando , temos .
Daí:
Portanto:
(o que importa aqui é que a reta irá passar pelo eixo em ).
Vai ser algo assim:
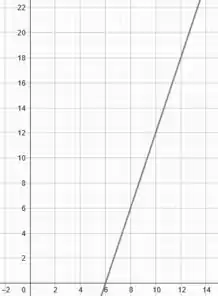
Sacaram?
O nosso objetivo é ajustar o coeficiente dessa reta de modo que ela tangencie a parábola. Quanto tivermos a tangência, significa que o passageiro e o trem terão apenas um ponto de encontro. Caso contrário, se a reta cortasse a parábola, o passageiro e o trem teriam dois pontos de encontro, e aí o passageiro teria uma velocidade maior do que a necessária.
Esse é o nosso trabalho gráfico, conseguir fazer essa ajuste com muito esmero e cuidado 😊
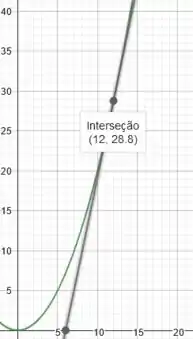
Encontramos essa condição para a reta:
Ou seja, a velocidade mínima que o passageiro precisa assumir é:
Prontinho!
Curtiram a solução? Responde Aí!