UFABC – Fenômenos Mecânicos – P2 – Questão 1
Um estudante está de pé sobre um penhasco vertical acima da entrada de uma caverna. Ele sente batendo no rosto um vento muito forte, e decide chutar uma bola horizontalmente, contra o vento, de forma que ela acabe caindo na entrada da caverna. Assuma que o vento vai gerar na bola uma aceleração horizontal de módulo , e assuma que, exceto por esse efeito, a resistência do ar na direção vertical pode ser desprezada.
Proponha uma fórmula para a velocidade com que o menino precisa chutar a bola para conseguir realizar seu feito.
Desenhe a forma aproximada os vetores velocidade e aceleração da bola no ponto em que a bola está mais distante da parede do penhasco.
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas estou aqui para te ajudar! Vamos resolver juntos?
Para resolvermos essa questão, precisamos entender que tipo de movimento estamos lidando (MRU ou MRUV) nas direções vertical e horizontal
E lembrar que a variável em comum aos movimentos é sempre o tempo. A bola desce a mesma medida que se movimenta para o lado, então o tempo é o mesmo nos dois movimentos.
O menino quer chutar a bola de forma que ela caia na porta da caverna, então horizontalmente ela vai sair do zero e chegar no zero. E isso só é possível em duas situações:
- quando o objeto está em repouso (sim, se ele não se move, ele está no zero e segue estando...)
- e quando a velocidade inicial e a aceleração estão em sentidos opostos (que é a situação de quando eu jogo uma bola pra cima... a velocidade inicial é positiva, mas a gravidade aponta pra baixo, e vai trazer a bola pro mesmo lugar)
No nosso caso a velocidade inicial da bola é positiva (vou adotar horizontal para direita como sentido positivo tá?) e a aceleração é contra o vento, ou seja, contra nossa velocidade inicial. Assim a bola vai descrever uma parábola no ar à medida em que desce o penhasco em direção ao chão.
Saca só nesse desenho aqui:
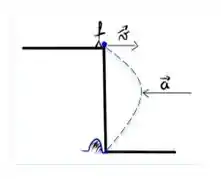
Com a aceleração horizontal a bolinha até começa o movimento indo pra frente, mas volta ao seu ponto de origem. Então na direção horizontal estamos lidando com um MRUV.
E na vertical? Bom, como é uma queda, sempre temos a ação da gravidade. A gravidade é uma aceleração que aponta sempre para baixo. Então estamos também lidando com um MRUV na direção vertical.
A velocidade inicial é puramente horizontal, e é ela que queremos descobrir.
Beleza?
Passo 2
Vamos agora ver os dados que o problema nos diz. Na vertical (MRUV com a=-g) temos o seguinte:
- altura inicial:
- Velocidade inicial:
E com essas informações podemos descobrir o tempo de queda da bola até ela chegar no chão. Assim podemos fazer na equação da posição! A equação da posição em função do tempo é
Substituindo os valores temos:
Tranquilo até aqui?
Passo 3
Tá, mas nosso objetivo é encontrar a velocidade inicial! Como falei lá no início, o tempo é o mesmo! Então agora quando formos olhar para a horizontal, já podemos usar o resultado do passo anterior!
Na horizontal temos que a bolinha sai do zero (admitindo que o zero seja a entrada da caverna) e volta para o zero. Temos a aceleração, o tempo e queremos saber a velocidade inicial. Então vamos usar de novo a equação para a posição do MRUV, mas aplicada para a horizontal, saca só:
Aqui a aceleração é contrária ao sentido positivo, então vou colocar um sinal de ali na equação. Temos também que a bola sai e volta para o mesmo lugar então . Aí a equação fica assim:
E isolando temos:
E o tempo? Ah! Aqui vou usar o resultado do passo anterior!
Como o movimento é o mesmo, apenas dividimos ele pra poder calcular melhor as quantidades. Aí encontrando o tempo na direção vertical, é só usar aqui na horizontal!
Lembrando que o tempo de queda é:
E a velocidade inicial:
Daí temos:
Então a velocidade inicial deve ser .
Beleza? Espero ter te ajudado!