Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento Retilíneo Uniformemente Variado

Ver Teoria
Exercício 951234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939496979899100

Enunciado

Um móvel parte da origem do movimento com velocidade 2   m / s e aceleração 4   m / s 2 durante 5   s . Em seguida mantém-se em velocidade constante durante 2   s . Logo após o móvel começa a reduzir sua velocidade a uma taxa de 3   m / s 2 até parar.

A) qual o deslocamento total do móvel.

B) qual a velocidade média do móvel durante o deslocamento.

OBS: Efetue o arredondamento em 1 (uma) casa decimal.

Passo 1

Vamos entender o que está acontecendo aqui!!

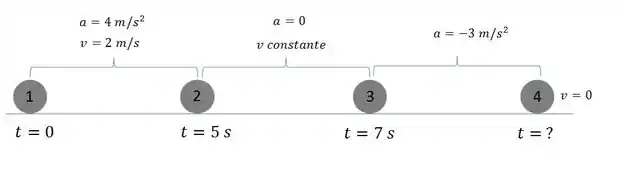
De 1 pra 2, passaram 5   s , e o movimento durante esse tempo começou com uma velocidade inicial de 2   m / s , e com uma aceleração de 4   m / s 2 . Beleza? Então é um movimento uniformemente variado-MUV.

De 2 pra 3, temos um movimento com velocidade constante, um movimento uniforme-MU. Ah! E qual vai ser essa velocidade constante? Vai ser 2   m / s ? Não!!! Vai ser a velocidade final da primeira parte do movimento, ou seja, a velocidade que o móvel tem em t = 5   s . Beleza?

De 3 pra 4, temos uma desaceleração. Não sabemos quanto tempo demora até o movél parar, mas sabemos que a velocidade final é zero. Beleza?

Esse também é um MUV.

Ok então. As equações do MUV são:

S = S 0 + v 0 t + 1 2 a t 2

E

v = v 0 + a t

Para o movimento uniforme:

S = S 0 + v t

Show?

Passo 2

(A)

Vamos começar vendo como a nossa posição S   tá mudando com o tempo.

De 1 pra 2 (MUV):

S = S 0 + v 0 t + 1 2 a t 2

S 0 = 0 , pois ele sai da origem. A velocidade inicial é 2   m / s , e a aceleração é 4   m / s 2 .

S = 0 + 2 t + 1 2 4 t 2

Depois de 5   s :

S = 0 + 2 ( 5 ) + 1 2 4 5 2

Resolvendo isso, temos:

S = 60   m

Como a velocidade tá variando, vamos calcular a velocidade que o móvel tem quando t = 5   s , pois essa será a velocidade inicial do movimento de 2 para 3.

v = v 0 + a t

v = 2 + 4 ( 5 )

v = 22   m / s

Beleza. Agora, para a parte de 2 para 3, temos um MU. Então,

S = S 0 + v t

S 0 é o que a gente já andou até agora, que foi 60   m . Então, no final de 2   s , vamos ter:

S = 60 + 22 2

S = 104   m

Beleza, até agora já andamos 104   m . Vamos lá!! Falta pouco!

Para a parte de 3 para 4, temos um MUV.

A gente precisa descobrir quanto tempo esse movimento demora. Sabemos a velocidade final (zero, porque ele para), a velocidade inicial, que é 22   m / s , já que o movimento anterior foi uniforme, a velocidade não variou, e sabemos também a aceleração, então:

v = v 0 + a t

0 = 22 + - 3 t

t = 22 3 s

Beleza! Agora é só ver qual é a posição do móvel depois de ter passado esse tempo:

S = S 0 + v 0 t + 1 2 a t 2

S = 104 + 22 22 3 + 1 2 - 3 22 3 2

Resolvendo isso, temos:

S = 184,7   m

Uhuul!!

Passo 3

(B)

Agora, queremos a velocidade média:

v m = ∆ S ∆ t

Acabamos de calcular o deslocamento, então:

∆ S = 184,7   m

E o intervalo de tempo total é:

∆ t = ∆ t 1 → 2 + ∆ t 2 → 3 + ∆ t 3 → 4

∆ t = 5 + 2 + 22 3

∆ t = 14,3   s

Então:

v m = ∆ S ∆ t

v m = 184,7   14,3

Então:

v m = 12,9   m / s

Resposta

(a) S = 184,7   m

(b)

v m = 12,9   m / s

Exercícios de Livros Relacionados

Você está discutindo no telefone celular enquanto segue um carro de polícia não identificado, a 25m de distância; os dois veículos estão a 110k m / h . A discussão distrai sua atenção do carro de polí
Um trem vermelho a 72k m / h e um trem verde a 144k m / h estão na mesma linha, retilínea e plana, movendo-se um em direção ao outro. Quando a distância entre os trens é 950m , os dois maquinistas per
O bloco da Figura 5.14 desliza sem atrito da altura h = 10 m, partindo do repouso. Sendo ∅ = 30 ° , calcule:A) O tempo gasto no deslizamento até o fim da rampa.B) A velocidade final do bloco.
Um trem de metrô parte do repouso em uma estação e acelera com uma taxa constante de 1,60m / s 2 durante 14,0s . Ele viaja com velocidade constante durante 70,0s e reduz a velocidade com uma taxa cons
No lançamento, a nave espacial pesa 4,5 milhões de libras. Quando lançada a partir do repouso, leva 8,0 s para atingir 161k m / h e, ao final do primeiro minuto, sua velocidade é 1610k m / h . a) Qual