UFSCAR, Sem Campus, Física 1, AV1 - 2021.1 - Prof° Raphael Santarelli, Questão 1c
Na célebre corrida entre a lebre e a tartaruga, a velocidade da lebre é de e a da tartaruga de . A distância total a percorrer é de em linha reta. Depois de a lebre para e tira uma soneca de minutos, e depois acorda e continua com a mesma velocidade anterior de . Deixe todas as respostas em unidades do SI.
Em quais instantes a tartaruga e a lebre se cruzam? Quais as posições delas nesses instantes?
Passo 1
Oiie, tudo bem com você?
O professor desta vez buscou nos dar uma representação física da fábula da tartaruga e da lebre! Então, vamos ver se a tartaruga realmente vai ganhar! Primeiro ele nos dá a velocidade de cada um dos animais, a tartaruga tem a seguinte velocidade constante
o valor está em metros por minuto, então vamos ter que convertê-lo para o SI (metros por segundo) posteriormente, belezinha? A velocidade da lebre no entanto, não é constante no tempo, temos que ela inicialmente tem a velocidade
mas, após minutos, a lebre tira uma soneca, ou seja, sua velocidade vai a zero por . Após esta soneca, ela continua a corrida com a sua velocidade inicial! A corrida é um percurso de . Esta alternativa quer os instantes de tempo em que elas se cruzam, e as posições delas nestes instantes de tempo. Ótimo! Nas alternativas anteriores nós construímos as equações horárias de movimento de ambas como
e, também que
Apenas com estas informações é possível determinar os pontos de cruzamento e as posições que a alternativa pede! No entanto, nós também obtivemos na alternativa anterior o seguinte gráfico
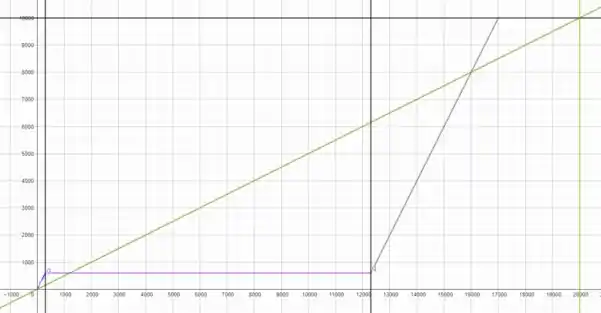
em que a reta verde inclinada indica o movimento da tartaruga, que chega na linha de chegada (reta horizontal preta) em (reta vertical verde). A junção da reta azul, reta rosa e reta cinza, indicam o movimento da lebre, em que as retas verticais pretas indicam o tempo em que ela tira uma soneca! Vamos usar essas informações em nossa questão!
Passo 2
Como vemos no gráfico do passo , a tartaruga e a lebre se interceptam quando a lebre está em sua soneca, ou seja, a reta verde intercepta o segundo intervalo da equação de movimento da lebre. De forma, que para saber em que instante de tempo isso ocorre, precisamos
em que é a equação do segundo intervalo da equação de movimento da lebre, dada por
Usando a equação do movimento da tartaruga, temos que
Se isolarmos o tempo, obtemos então que elas se cruzam em
em que a lebre está na sua soneca na posição , e a tartaruga, naturalmente, também! Vamos agora ver a segunda intersecção! Saca só!
Passo 3
Se olharmos o gráfico no passo , vemos que agora é uma ultrapassagem da lebre que está se movendo no terceiro intervalo, portanto, vamos precisar fazer a seguinte igualdade
em que
em que é o instante de tempo que a lebre termina a corrida! Usando novamente a equação de movimento da tartaruga, temos que
Isolando o tempo de um lado, e as constantes de outro, temos que
portanto, isolando o tempo, temos que
é o instante em que eles se cruzam. E, usando a equação da tartaruga (por simplicidade), temos que a posição é a seguinte
que é a posição em que a segunda intersecção acontece! É tartaruga, foi quase dessa vez! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Elas se interceptam nos tempos e , nas posições e .