Na célebre corrida entre a lebre e a tartaruga, a velocidade da lebre é de e a da tartaruga de . A distância total a percorrer é de em linha reta. Depois de a lebre para e tira uma soneca de minutos, e depois acorda e continua com a mesma velocidade anterior de . Deixe todas as respostas em unidades do SI.
Escreva as equações de movimento para a lebre e para a tartaruga.
Desenha as curvas da posição em função do tempo da tartaruga e da lebre (no mesmo gráfico). Quem ganha a corrida?
Passo 1
Oiie, tudo bem com você?
O professor desta vez buscou nos dar uma representação física da fábula da tartaruga e da lebre! Então, vamos ver se a tartaruga realmente vai ganhar! Primeiro ele nos dá a velocidade de cada um dos animais, a tartaruga tem a seguinte velocidade constante
o valor está em metros por minuto, então vamos ter que convertê-lo para o SI (metros por segundo) posteriormente, belezinha? A velocidade da lebre no entanto, não é constante no tempo, temos que ela inicialmente tem a velocidade
mas, após minutos, a lebre tira uma soneca, ou seja, sua velocidade vai a zero por . Após esta soneca, ela continua a corrida com a sua velocidade inicial! Se o percurso é de , a questão é bem direta! Quem ganhou? Nós vamos fazer isso utilizando a forma da equação horária do movimento para velocidade constante, ou seja
e, fazer o plot do gráfico para cada uma das curvas! Vem comigo!
Passo 2
A velocidade da tartaruga é constante, portanto, podemos simplesmente aplicar a equação horária do movimento que dei no passo , escolhendo um referencial de forma que e , e também que , temos que
A equação acima está considerando que é dado em minutos, vamos converter as unidades para estarmos no sistema internacional de metros por segundos. Se lembrarmos que
podemos substituir em nossa velocidade que
e, a equação do movimento em unidades do SI é tal que
Maravilha! Agora, vamos construir algo parecido para a lebre! Saca só!
Passo 3
A lebre em geral não tem velocidade constante, mas, nos intervalos em que ela está se movendo, sua velocidade é constante. Portanto, podemos dividir a nossa equação do movimento em três partes! Primeiro, temos que
após minutos a lebre irá tirar uma soneca, então a sua equação do movimento será da forma
em que . Após minutos a lebre lembra que está em uma corrida, e portanto, volta a se mover, e sua equação de movimento volta ao formato
mas note que , já que a lebre não se moveu em todo esse período de tempo! Consegue montar a equação de movimento como um todo usando as informações acima? Bora lá!
Passo 4
Escolhendo o mesmo referencial que a tartaruga, ou seja, e , temos que
em que temos que o tempo está indicado em horas! Para estarmos no sistema internacional, vamos lembrar que , ou seja, temos
e, como temos que , podemos substituir em nossa velocidade para obter
Então, no sistema internacional de unidades, temos que a primeira parte da equação de movimento da lebre é
Precisamos construir agora uma equação para os dois outros intervalos! Saca só!
Passo 5
Como discutimos antes, temos que a segunda parte da equação de movimento é tal que
como temos que , mas lembre-se que escrevemos em unidades do SI, portanto, precisamos usar que . Temos então que
ou, simplesmente
esta, é a equação de movimento da segunda parte, note que não depende do tempo, naturalmente, já que a lebre não se moveu no intervalo de tempo que a equação acima tem validade! Agora, para a última parte da equação, temos que
Lembrando que , podemos escrever
Maravilha! Juntando os três resultados, e usando que temos que a equação de movimento da lebre é
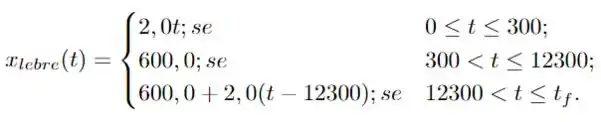
em que é o instante de tempo em que a lebre termina os da corrida! Ótimo! Agora é só juntarmos a equação de movimento da tartaruga e da lebre! E, veremos finalmente quem venceu! Bora lá!
Passo 6
O gráfico de ambas as funções em conjunto é o seguinte
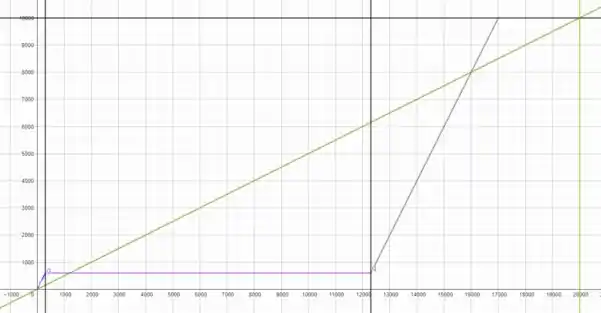
A reta verde é o movimento da tartaruga, no que ela alcança em (reta vertical verde). O movimento da lebre é dado pelo conjunto da pequena reta azul que termina em (primeira reta vertical preta). Então, a soneca da lebre é representada pela reta rosa horizontal, quando esta reta chega em (segunda reta vertical preta), a lebre começa a se mover novamente. Note, que a reta cinza final representando o movimento da lebre chega em em , por mais que as fábulas tentem nos dizer, a lebre ainda ganhou da tartaruga!
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
As equações de movimento são
e,
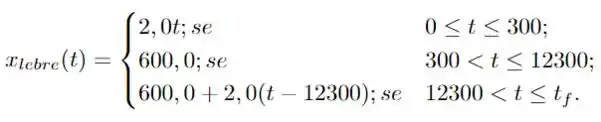
Pelo gráfico, temos a vitória da lebre!