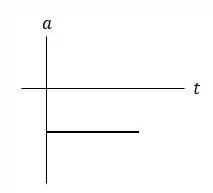UnB - Física 1 - Listas - Lista 2 Movimento em uma dimensão - Questão 5d
Do topo de um prédio, um estudante arremessa um balão d’água verticalmente para baixo. O balão deixa a mão dele com velocidade igual a Desconsidere a resistência do ar para que o balão esteja em queda livre assim que abandona a mão do estudante.
Esboce os gráficos , , e para o movimento.
Passo 1
Falaa, gente linda! Tudo certo com vocês? Essa questão parece complicadinha, mas aqui a gente transforma ela em algo mais tranquilo hahaha bora, juntos??
Bom temos que um estudante arremessou um balão com água verticalmente para baixo com uma velocidade e agora estamos interessados nos gráficos desse movimento, assim temos que esboçar os gráficos , , e . Sabendo que a velocidade inicial com que o balão é abandonado é de .
Galerinha, como o movimento em questão é de queda livre temos que a aceleração da nossa questão é a da gravidade, portanto constante e igual a . Não só, mas também podemos afirmar que por ser um movimento de queda livre todas as fórmulas definidas para o Movimento Uniformemente Variado(M.R.U.V) são válidas para cá.
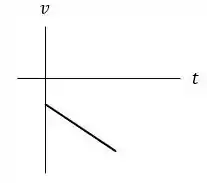
Assim, para conseguirmos modelar o gráfico precisamos das equações, começaremos encontrando a equação da velocidade a partir da função horária da velocidade para o M.R.U.V:
Substituindo os valores com os dados da nossa questão, lembrando que o sentido adotado para analisar esse movimento será:
O gráfico é uma reta uma vez que a função encontrada é da forma , para montar o gráfico podemos utilizar um software gráfico ou utilizar uma tabelinha de valores para traçar o esboço de qualquer uma das formas o resultado será:
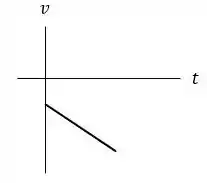
Passo 2
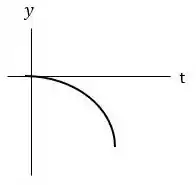
Já para encontrarmos a posição em função do tempo iremos utilizar a fórmula da posição para o M.R.U.V:
Substituindo os valores:
Graficamente essa função representa uma função do segundo grau do tipo , ou seja, o esboço será uma parábola com a concavidade voltada para baixo.
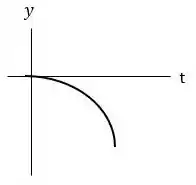
Pessoal a posição tem que ser negativa mesmo, como o nosso referencial é o solo a medida que o objeto caí suas posições em relação ao referencial vão diminuindo cada vez mais até atingir o solo.
Passo 3
Por fim, temos o gráfico da aceleração. Como já mencionado anteriormente a aceleração no movimento de queda livre é constante e igual a gravidade . Logo o gráfico em função do tempo será uma reta de valor . Ela será negativa devido ao fato de o sentido positivo da nossa análise estar apontado para cima.
Assim,
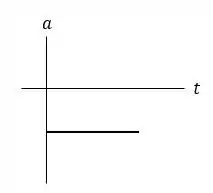
E é isso xuxus! Qualquer dúvida manda aí que a gente Responde! :)
Se cuidem! Tchauzinho
Resposta
