UFMG; Fundamentos de mecânica; Provas – P1; 2022.1; Questão P1.1
Na figura ao lado vê-se uma montagem. A bolinha de massa é lançada para cima por uma rampa que faz um ângulo com a horizontal, saindo da rampa a uma altura a partir do solo. Mede-se que a bolinha leva um tempo para atingir o solo, a partir do instante que sai da rampa.
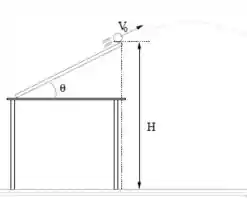
P1.1 – Calcule o módulo da velocidade da bolinha no instante que ela saiu da rampa, , em função de g, , , e .
Passo 1
Faaaala galera! Tudo certinho com vocês?? Bora lá resolver mais um probleminha!
Nessa questão, temos uma rampa inclinada de um ângulo cujo ponto mais alto está em uma altura .
Daí, uma pessoa muuuuito ocupada haha resolve lançar uma bolinha nessa rampa, de modo que o tempo de queda a partir do instante que a bolinha perde o contato com a rampa até o momento que toca o solo vale . Beleza até aqui?
O objetivo do exercício é encontrar a velocidade que a bolinha possui ao perder o contato com a rampa. Como podemos fazer isso?
Passo 2
Primeiramente meus jovens, a bolinha, após sair da rampa, movimenta-se com velocidade constante na horizontal e com velocidade uniformemente acelerada na vertical. A equação que rege a posição na vertical em função do tempo é dada por:
Pelo o enunciado da nossa questão sabemos que a inclinação da rampa é dada por e que a velocidade é decomposta em duas como observado na imagem abaixo:
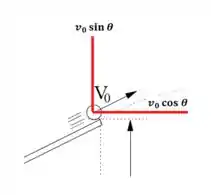
Assim a gente tem que:
Sabendo então que a bolinha atingiu o solo no tempo após sair da rampa, e considerando o solo como sendo a origem, podemos escrever:
Dessa forma, isolaremos o valor de que é o que se pede na questão:
E com isso temos nosso resultado de em função das variáveis g, , , e . Note que a massa não entra na nossa questão!
Maneirinho?? Te vejo na próxima!