Você está em um elevador panorâmico indo do andar térreo para o décimo primeiro andar quando, ao passar pelo segundo andar, que está a metros do andar térreo, percebe que uma lâmpada se soltou do teto do elevador. A lâmpada está a metros do piso do elevador e a velocidade constante do elevador é de . Assuma
a) Quanto tempo a lâmpada leva para bater no piso do elevador?
b) Uma pessoa posicionada no andar térreo observa a queda da lâmpada. Faça os gráficos de e que esta pessoa observou para o intervalo de até o tempo em que a lâmpada bate no chão do elevador.
c) Agora faça esses gráficos de e para a sua observação de dentro do elevador.
Passo 1
Quando iniciamos o problema, temos que ter em mente que galileu está nos observando e toda vez que erramos, ele se revira em seu tumulo, então cuidado hahaha ... Todo problema de física se resume em, à de onde estamos observando, ou seja, nosso referencial.
Passo 2
(a) Nosso primeiro item observe que estamos dentro do elevador observando a lâmpada. Desta forma colocamos nosso referêncial no chão do próprio elevador
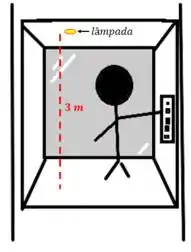
Como o elevador sobre com aceleração constante igual a zero, podemos tratar o problema como um simples problema de queda livre. Assim pelo nosso famoso sorvetão, temos que
Sabemos que , sabemos que e também sabemos que no referencial de quem está dentro do elevado, , então
Que implica em
Passo 3
(b) Diferente da pessoa que está dentro do elevador, uma pessoa observando de fora vê que a lâmpada se move com a mesma velocidade que o elevador, ou seja
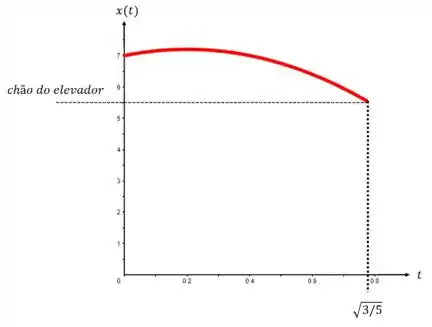
No momento em que a lâmpada se solta, podemos dizer que o observador de fora começa a descrever seu movimento. Pela nossa equação da posição em função do tempo, temos que
Na qual , e
Ou seja
Legal, mas em que momento a lâmpada toca o chão? Perceba que o tempo de queda já foi calculado no primeiro item e foi , assim
Resolvendo
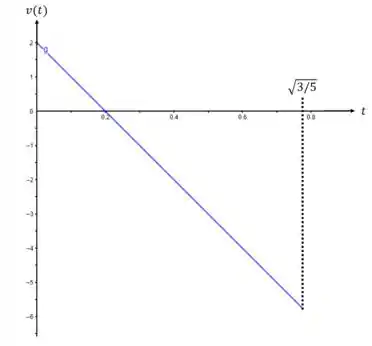
Agora com relação a velocidade, tomando a derivada da posição em função do tempo e temos
Que resulta em
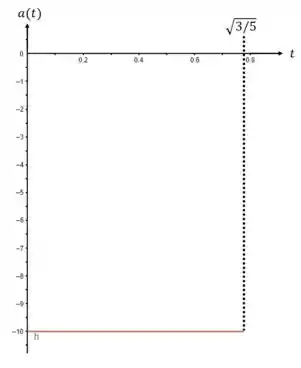
E consequentemente
Passo 4
(c) Agora queremos os gráficos que indicam a observação do observador dentro do elevador. Do primeiro item temos a posição em função do tempo
Que já tínhamos determinado com . Então ...
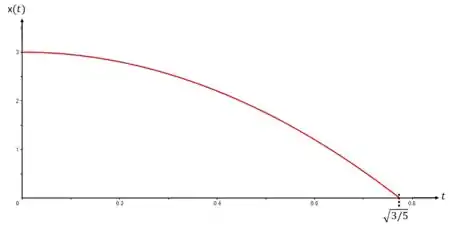
Agora para a velocidade, temos que
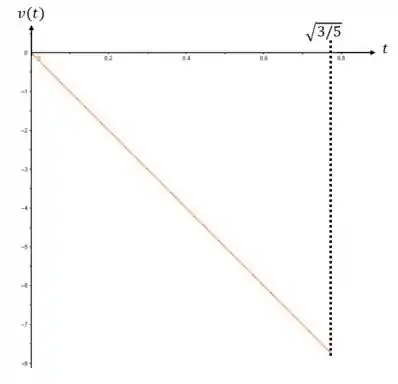
E finalmente temos que
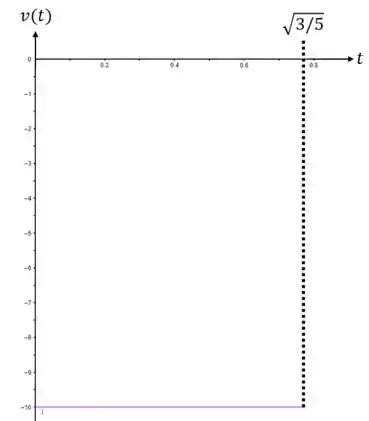
Resposta
- , e
- , e