![]()
Passo 1
Para resolver essa questão, vamos utilizar o teste da integral. Sendo:
Façamos:
Lembre-se de que é um número fixo, a variável é .
Passo 2
Vamos calcular a integral em um intervalo finito:
Sabendo que:
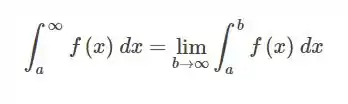
Vamos tomar o limite considerando os dois casos a seguir:
Caso 1:
Nesse caso, , porque o expoente é positivo. Assim, o limite da expressão é infinito e a integral diverge.
Pelo Teste da integral, a p-série diverge.
Caso 2:
Nesse caso, , porque o expoente passa ser negativo. Assim:
Como a integral converge, nesse caso, pelo Teste da integral, a série também converge.
Não considerei o caso em que , pois teríamos zero no denominador. Para esse valor, a p-série se torna uma série harmônica, que já provamos na teoria que diverge.
Resposta
A série converge para e a série diverge para .