UFCG, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - UAMat - Lista 4, Questão 9i
9 - Determine se a série converge ou diverge.
i)
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema queremos determinar se a serie dada por converge ou diverge.
Parece de boa? 🤔
Para resolver esse problema, podemos aplicar o teste da integral para ver se a série converge ou diverge.
O teste da integral consiste em, dada uma série , substituir por para obter uma função e integrar em .
Assim se a integral converge, converge, mas se a integral diverge, também diverge.
Sacou? Bora começar! 😉
Passo 2
Nesse caso,
Substituindo por , temos
Calculando a integral de
Nesse caso, podemos usar uma abordagem diferente... se esboçarmos o gráfico de , vamos obter
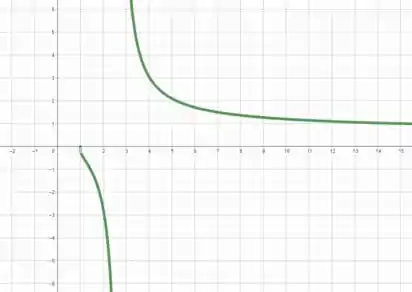
Perceba que em , temos
Ou seja, em temos uma descontinuidade... para valores infinitesimalmente menores que tende a e para valores infinitesimalmente maiores que tende a . Portanto podemos dizer que temos uma divergência.
Logo, se a integral diverge, a série também diverge!
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
Diverge pelo teste da integral.