11 - Considere um plano infinito, uniformemente carregado, coincidente com o plano XY e um dado sistema de coordenadas. Sobre o campo elétrico produzido por este plano, considere as afirmativas abaixo:
- é independente das coordenadas x e y.
- A direção de é paralela ao eixo Z em todos os pontos do espaço.
- aponta no mesmo sentido em todos os pontos do espaço.
São VERDADEIRAS as afirmativas:
- Apenas II
- Apenas I e III
- Apenas III
- I, II e III
- Apenas I e II
Passo 1
Ora, um plano infinito de cargas no plano XY é como o plano da figura abaixo:
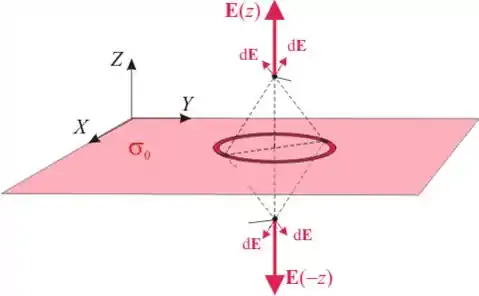
E perceba que aquele anel ali específico gera um campo elétrico total na direção de . Se você aumentar tanto quanto o raio interno e externo desse anel, o campo continua na direção de . Se você colocar o raio indo para o infinito, apenas o módulo do campo irá aumentar, mas a direção, ainda será o eixo , saca?
Agora, se você escolher outro qualquer no plano para centralizar o anel de cargas...
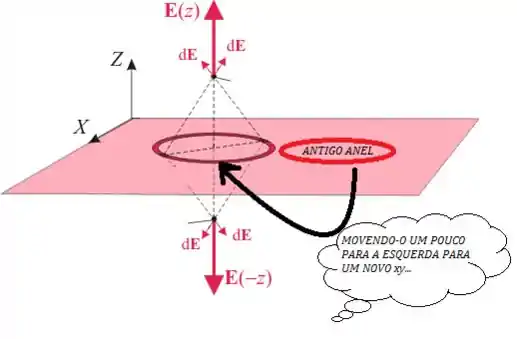
Perceba que o campo elétrico continua sendo o mesmo, afinal, com infinitas cargas em todo o plano, não importa onde você centraliza o seu anel, que ele sempre dará o mesmo valor para o campo elétrico em uma altura do plano (o que prova que o campo de fato não depende das coordenadas e do plano).
Então, o campo só depende de , saca? Logo, o Item I está correto.
Passo 2
O item II também está correto, pois em qualquer ponto, o campo sempre aponta na direção do eixo Z (perpendicular ao plano XY).
Para mostra isso, observe que as cargas de lados opostos do anel geram também de lados opostos...
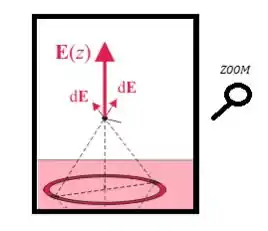
Cada uma dessas , possuem componentes opostas paralelas ao plano (componentes em azul):
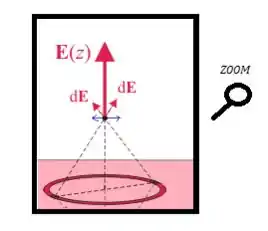
Como elas possuíram o mesmo módulo, pois o ponto pretinho está no centro do anel de cargas, essas componentes se cancelaram. Mas as componentes de em (aqui de verde):
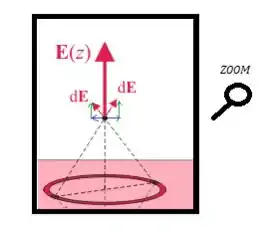
Somam-se!
Por isso, o campo elétrico possuirá apenas componentes em o tornando sempre paralelo a esse eixo! ;)
Passo 3
Ora, o plano tem dois lados, um em cima e outra em baixo!
O de baixo gera campos para baixo:
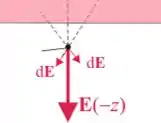
Assim como no item anterior, as componentes paralelas ao plano se cancelam devido as simetria oposta dos , já as componentes em apontando para baixo se somam, ficando um campo resultante negativo, claro, abaixo do plano:
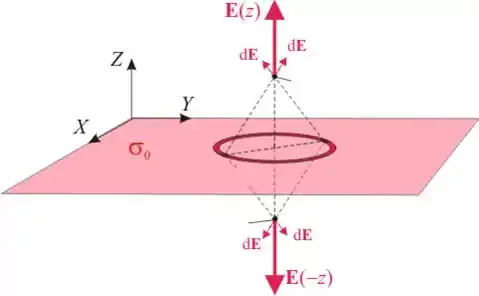
Nos pontos acima do plano, como já vimos, ele aponta para cima. Concluímos então que o campo não tem a mesma direção em todos os pontos do espaço (depende se o ponto está em cima ou em baixo)
Item FALSO!
Resposta
Letra E.