Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Gerado por uma Linha de Cargas

Ver Teoria
Exercício 8012345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879818283848586

Enunciado

UFRJ – Física 3 2020.2 – P1 – Questão 35

R , está centrado na origem e ocupa a porção superior do plano x y , como mostrado na figura abaixo. Ele possui uma densidade linear de carga constante e positiva λ . Considere um elemento infinitesimal de carga d q do semianel na posição definida pelo ângulo polar ϕ , como indicado. Este elemento compreende uma porção de ângulo infinitesimal d ϕ . Considere o ponto P mostrado na figura, localizado no eixo z a uma distância z da origem. Assinale a alternativa que representa a expressão da componente z do campo elétrico infinitesimal produzido por este elemento no ponto P .

Escolha uma:

  1. – k 0 λ R 2 + z 2 3 2 z R   c o s ϕ d ϕ
  2. – k 0 λ R 2 + z 2 3 2 R 2 d ϕ
  3. – k 0 λ R 2 + z 2 3 2 R 2   c o s ϕ d ϕ
  4. – k 0 λ R 2 + z 2 3 2 z R d ϕ
  5. – k 0 λ R 2 + z 2 3 2 z R   s e n ϕ d ϕ
  6. 0

Passo 1

Fala galera, tudo bem? Essa questão parece complicada, mas vou te ajudar a resolver, saca só!

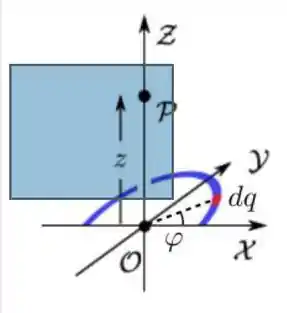
Quando pegamos apenas um pedaço do semianel, a carga nesse pedacinho é d q = λ d l . A componente z é proporcionao ao cosseno do ângulo com o eixo x . Então temos o seguinte:

c o s θ = R d = R z 2 + R 2

Passo 2

A distância do ponto P até o elemento de fio é:

d 2 = ( z 2 + R 2 )

E o elemento de comprimento d l , em função do ângulo polar é:

d l = R c o s ϕ   d ϕ

Passo 3

Agora vamos começar a juntar todas essas informações:

d E z = d E   . c o s θ = k 0 d q d 2   . c o s θ

E resgatando as informações dos passos anteriores temos:

d E z = k 0 λ d l ( z 2 + R 2 ) . R z 2 + R 2

E por fim substituímos d l e reorganizamos:

d E z = k 0 λ R c o s ϕ R z 2 + R 2 3 / 2

d E z = k o λ R 2 c o s ϕ d ϕ z 2 + R 2 3 / 2

E a direção? É negativa, pois o semianel está carregado positivamente e produz um campo com componente z negativa:

d E z = - k o λ R 2 c o s ϕ d ϕ z 2 + R 2 3 / 2

Beleza?

E analisando as alternativas, a correta é a (c).

Espero ter ajudado!

Resposta

( c )

Exercícios de Livros Relacionados

Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri