Densidade de Carga, Campos Elétricos e Corpos Carregados
A figura abaixo mostra dois arcos de circunferência cujo centro está na origem de um sistema de coordenadas. Em cada arco a carga está uniformemente distribuída.
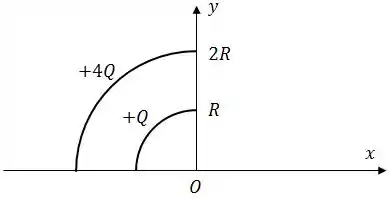
Determine:
O vetor campo elétrico para cada arco na origem;
O vetor campo elétrico total na origem (dê a sua orientação em relação ao semi-eixo positivo);
Passo 1
O vetor campo elétrico para cada arco na origem;
- Arco menor:
- Arco maior
- Arco menor
- Arco maior
O primeiro passo aqui é escrever a expressão do campo elétrico gerado por uma pedaço infinitesimal do arco, de carga :
Graficamente, a ideia é essa:
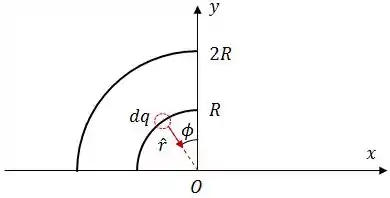
Daqui podemos tirar algumas coisas:
Além disso, podemos dizer que:
Onde é a densidade linear de carga.
Substituindo esses caras na expressão de , teremos:
Passo 2
Pra terminar, temos apenas que integrar esse cara de até .
A densidade linear de carga pode ser escrita como:
Logo:
Passo 3
As únicas diferenças o arco menor para o arco maior é que agora o raio é , ao invés de , e a carga do arco é , ao invés de .
Então a única coisa que temos que fazer é pegar a expressão do campo elétrico do arco menor e, onde estiver , substituir por e onde estiver , substituir por . Logo:
Passo 4
O vetor campo elétrico total na origem (dê a sua orientação em relação ao semi-eixo positivo);
O campo elétrico total será a soma vetorial dos dois campo elétricos, logo:
Resposta
Resposta
Ei, a resposta está no passo a passo :)