Uma barra isolada, de comprimento , tem uma carga distribuída uniformemente ao longo de sua extensão, conforme a figura.

Determine o vetor campo elétrico no ponto , situado a uma distância da extremidade direita da barra;
Suponha que uma outra carga isolada puntiforme seja colocada num outro ponto distante da extremidade direita da barra. Determine o vetor campo elétrico no ponto devido apenas à carga isolada;
Determine, agora, o vetor campo elétrico total no ponto ;
Passo 1
Determine o vetor campo elétrico no ponto , situado a uma distância da extremidade direita da barra;
Beleza!
Pra resolver esse tipo de problema, vamos começar pegando, da barra, uma pedaço infinitesimal de carga e ver o campo elétrico produzido por ela.
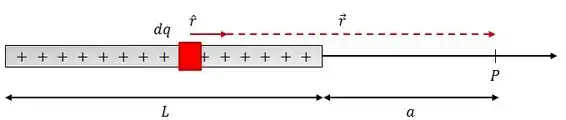
O campo elétrico gerado pelo elemento de carga é dado por:
Passo 2
Antes de voltarmos pra fórmula, repara que a carga infinitesimal pode ser escrita em função da densidade linear de carga .
Agora sim!
Passo 3
Agora é só integrar esse cara, onde:
Logo:
Como , podemos substituir de volta. Além disso, , logo:
Ah! Ao invés de , você poderia ter usado logo de cara também... não tem problema. Só procura desenhar o vetor pra especificar o jeito como você está usando ele.
Passo 4
Suponha que uma outra carga isolada puntiforme seja colocada num outro ponto distante da extremidade direita da barra. Determine o vetor campo elétrico no ponto devido apenas à carga isolada;
Opa! Agora ficou tranquilo, só alegria!
O campo elétrico gerado por uma carga pontual é dado por:
Como a carga é colocada a uma distância da extremidade direita da barra, ela vai estar a uma distância do ponto , como mostra a figura do enunciado.
Além disso, como a carga é positiva e está à direita do ponto :

Portanto, substituindo na equação do campo elétrico:
Passo 5
Determine, agora, o vetor campo elétrico total no ponto ;
Como o campo elétrico é uma grandeza vetorial, o campo elétrico total vai ser a soma vetorial dos campos que calculamos na letra e na letra :
Peraí! Só isso?!
Sim, só isso! ;)
Resposta