O arco de um quarto de circunferência de raio , mostrado na figura abaixo, possui uma distribuição de carga não uniforme dada por , sendo uma constante positiva.
(a) Calcule a carga total presente no arco, em função de e de .
(b) Calcule (em função de , de e da constante de Coulomb ) as componentes e com os respectivos sinais, do vetor campo elétrico criado pelo arco sobre o ponto localizado na origem.
Considere agora que o arco gere, em um ponto qualquer, um campo elétrico e que neste mesmo ponto seja colocada uma carga puntiforme .
(c) Encontre o vetor da força elétrica exercida pelo arco sobre a carga.
Passo 1
(a) O enunciado nos dá a distribuição de cargas, certo? Sabemos que essa distribuição é dada por:
Então, para termos a carga total, vamos integrar!
Substituindo em função da distribuição de cargas, temos:
Agora vamos usar a equação que o enunciado nos deu, que rege a distribuição e, junto dela, devemos substituir a variável que será integrada.
Resolvendo a integral, temos:
Passo 2
(b) É possível calcular as componentes do campo elétrico primeiramente em módulo e somente depois acrescentar os sinais corretos, mas aqui calculamos já com o sinal. Considere a figura:
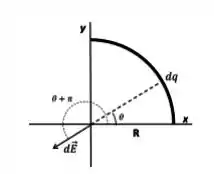
Vemos que e que . Assim:
Componente :
Sabemos que:
E também que:
Portanto:
Integrando:
Logo:
Já para a componente :
Usando as mesmas relações do :
Integrando:
Logo:
Passo 3
(c) A força elétrica exercida pelo arco sobre a carga é dada por:
Substituindo os valores:
Resposta
(a)
(b)
(c)